A solution to the single-question crowd wisdom problem论文简介及其笔记| 论文笔记好用的论文笔记工具

A solution to the single-question crowd wisdom problem

小木 Nature 2017-01 2371 2017/02/06 09:57:16

之前我们通过几篇论文讨论了预测市场的实际效果。简单来说，与bagging和boosting综合预测算法的想法类似，预测市场是将市场中不同个体对未来事件的预测综合起来得到比个体效果好的预测结果。这篇17年1月份的Nature文章主要讲述了当预测市场失效的情况，如何解决这个问题。

举一个简单的例子，假设你对美国的地理不了解，你遇到了一个问题：Philadelphia是不是Pennsylvania的州府？Columbia是不是South Carolina的州府？你把这个问题发送给很多人，让他们帮你回答，希望投票多的结果就是正确答案（这就是预测市场的基本思想）。在这里，我们把第一个问题称作是问题P，第二个问题称为问题C。对于第二个问题，采用这样的方法没有错，但是，对于第一个问题大部分人的回答都是错的。他们只知道Philadelphia是Pennsylvania历史上非常著名的一个很大的城市，但实际上，Pennsylvania的州府是Harrsiburg。这样的情况显然是预测市场方法本身的一个缺陷。
解决这样一个问题的方法是通过信任确定投票的权重。对于二分类问题来说，信任c是指回答者的投票有概率c的可能是对的，1-c的可能是错的（这个概率可以是回答者自己认为的）。但这个方法起作用的前提是正确的回答者被赋予了足够多的信任。但实际很难。在这里，作者通过一个替代的方案，他让人们预测别人在这个问题上的回答的分布，并选择那些得到足够多的支持的答案，而非预测的结果。这个算法的直观的理解如下：假设有两个可能的世界，一个世界是真实的，也就是Philadelphia并不是Pennsylvania的州府，另一个是假的世界，即Philadelphia是Pennsylvania的州府。可以理解的是，相比较那个假的世界，在真实的世界中，只有很少一部分人对这个问题的回答是yes。这可以用一个不均匀的投硬币来说明，也就是说在真实世界中，硬币上yes向上的概率是60%，而在假的世界中，硬币yes向上的概率是90%。在两个世界中，大多数的观点都是yes。人们知道这有偏差，但不知道哪个世界是真实的。因此，人们预测这个答案是yes的概率应该是60%到90%之间。然而，实际上对yes投票的概率将会收敛到60%。作者将这个概率选择的原则称为“surprisingly popular”算法，并在附件中给了严格的定义。在问题P中，数据显示，回答yes的人认为大多数人的想法和他们一样，而回答no的人则认为大部分人的回答和他们不一样。这样对于yes的平均预测结果是很高的，导致了实际中yes的比例要比预测结果低。因此，“surprisingly popular”的结果是no，答案正确。在问题c中则刚好相反，yes投票的预测要低于实际yes的投票，那么surprisingly popular的答案与popular的答案一样。
有没有一个有效的方法可以建立使用回答者的信任呢？假设回答者知道先验的世界概率和硬币的偏差。每个回答者通过观察自己的投币结果并运用贝叶斯准则计算他们的信任。这个假设需要从大量的抽样中识别实际的硬币。作者从理论上证明了并不存在这样的算法。通过比较，作者说明了SP算法有理论上的支撑，SP算法总会选择最好的答案呈现给大家。同时，作者做了四个类型的实验来证明这个方法的有效性。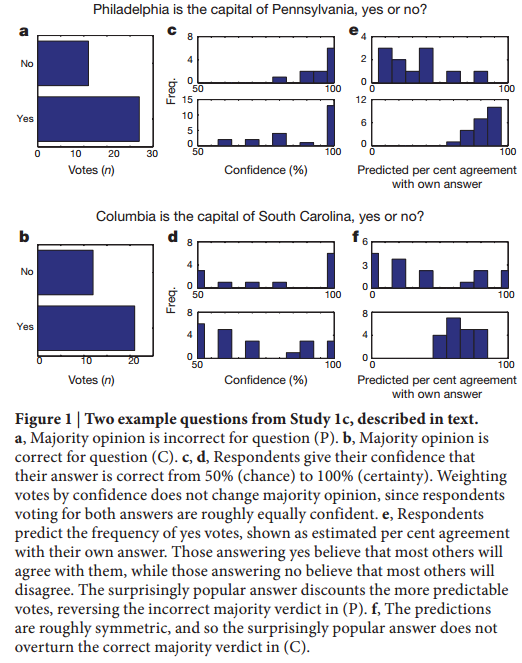
![](http://www.datalearner.com/resources/blog_images/11e376e7-374a-4b88-85f0-8cf9b83d7023.png)

赏

支付宝扫码打赏

如果文章对您有帮助，欢迎打赏鼓励作者