Learning from multiple annotators with varying expertise论文简介及其笔记| 论文笔记好用的论文笔记工具

Learning from multiple annotators with varying expertise

小木 Machine Learning 2014-06 2124 2017/02/06 09:55:17

这篇文章是之前说的那个Machine Learning专刊的一篇文章。

从多个标注来源或者知识源学习逐渐变成机器学习和数据挖掘中一个非常重要的问题。这主要是因为收集分项数据变得简单因而使得从群体中聚集推断知识变得重要。这篇文章主要是关注使用概率的方法来解决从多个来源学习的问题。作者认为，每个标注者都是不可靠的，因为他们观察的数据和专业知识都是不同的。本模型可以估计数据的实际标签。

废话不多说，直接上模型。

假设我们有N个数据点$X={\textbf{x}\_{1},...,\textbf{x}\_{N}}$，它们都是从一个输入分布中独立抽取的样本，每个数据点最多被T个标注者打上了标签。假设$Y={y\_{i}^{(t)}}$是用户的标注结果，其中$y\_{i}^{(t)}$表示第$i$个数据点，被标注者t标注的结果。作者假设这些标注不完全对，因此引入了新的变量，即所有数据的真实标签结果$Z={z\_{1},...,z\_{N}}$，这是未知的。
假设$x\_{i}$和$z\_{i}$（$i={1,...,N}$）是来自输入空间$\mathcal{X}$和输出空间$\mathcal{Z}$的随机变量。同样的，$y\_{i}^{(t)}$是标签的空间$\mathcal{Y}$。其中$t \in {1,...,T}$。在这里，我们假设所有的真实标签都是未知的（有些情况下部分是知道的）。
在给定训练集$X$和$Y$的条件下，作者的目标是求出$Z={z_1,...,z_N}$。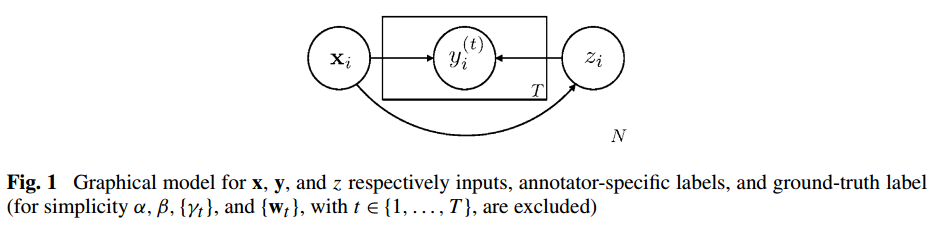

![](http://www.datalearner.com/resources/blog_images/2115ed36-6736-48d0-9811-3e8ed4563201.png)

####1、基本的概率模型
我们需要考虑很多元素，其中最关键的部分是如何为每个独立的标注者的个性建模，这些元素取决于什么，它对标注结果有什么影响？
在为多个标注者建模的时候，我们认为标注者主要依赖于未知的事实$z$和输入数据$x$进行判断。标注者被认为是与输入数据和真实标签之间相互独立。
也就是说，我们并不假设所有的标注者在标注的时候是具有一样的水平的，它应当取决于他们观察的结果。
因此，我们得到了一个联合条件分布：
```math
p(Y,Z|X) = \prod_{i}p(z_{i}|x_i) \prod_tp(y_i^{(t)}|x_i,z_i)
```
其实条件分布有很多，作者在这篇文章中探讨了几种情况：

#####1.1、最简单的情况
最简单的情况就是我们认为每个标注者$t$提供了一个相比较真实标签$z$的一个具有噪音的版本：
```math
p(y_i^{(t)}|x_i,z_i) = p(y_i^{(t)}|z_i) =(1-\eta^{(t)})^{|y_i^{(t)}-z_i|}\eta^{(t)^{(1-|y_i^{(t)}-z_i|)}}
```

这里$Z \equiv \mathcal{Y} = {0,1}$。在Bernoulli模型中，参数$\eta^{(t)}$是指标注者t是正确的概率。另一个选择是我们使用高斯模型，也就是假设标注者提供了一个队真实连续输出的扭曲版本：
```math
p(y^{(t)}|z_i) = \mathcal{N} (y_i^{(t)};z_i,\sigma^{(t)})
```

这里作者使用的是连续随机变量的分布，因为这符号回归的思想，而不是分类的思想。同时，这里作者假设$p(y\_{i}^{(t)}|x\_{i},z\_{i})$。这个假设表明这个图模型是和马尔科夫等价的模型。
在实际中，作者发现标注者的表现不仅受到自身专业水平的影响，也受到呈现的数据的影响。作者认为这只在非专业的标注者中出现的。

#####1.2、考虑数据的影响
作者使用了一个新的模型来考虑数据的影响，即：
```math
p(y_i^{(t)} | x_i,z_i) = \mathcal{N} (y_i^{(t)};z_i,\sigma_t(x_i))
```

在这里，方差受到了每个标注者和数据的影响。

赏

支付宝扫码打赏

如果文章对您有帮助，欢迎打赏鼓励作者