Optimizing Semantic Coherence in Topic Models论文简介及其笔记| 论文笔记好用的论文笔记工具

Optimizing Semantic Coherence in Topic Models

小木 EMNLP 2011-07 4519 2017/02/06 09:57:05

统计话题模型，例如LDA是一种非常强大的分析文本的工具。但是现有的话题模型有很多问题，比如话题质量评价等。作者的这篇论文主要有三个贡献：1）提出了一种识别低质量话题的方法；2）提出了一种识别这种话题的自动评价矩阵，且不依赖于人工的标注或者训练集；3）提出了一个新的统计话题模型，可以显著的提高话题质量。作者的实验数据是NIH。
##### 话题数量与质量之间的关系
通常情况下，用户都习惯于选择发现较多的话题数量来获取更好的解决方案，然而，作者发现话题数量与话题质量之间具有很强的关系：随着话题数量的增长，最小的话题（即该话题下词语的数量）的质量总是很差。传统的话题模型的评价主要依赖于外部方法（如利用发现的话题做信息抽取等）或者是定量的内部方法（例如计算held-out文档的概率）。最近的工作则主要集中在语义一致性的概念。比如Chang等人发现held-out并不与人工判断一致，Newman等人则提出了以基于次贡献的统计方法预测话题质量，AlSumait等则利用话题之间分布的差异来识别无意义的话题，还有Andrzejewski等人则提出了一种半监督的方法来避免用户标注。
作者首先邀请两位专家一起人工标注了NIH数据的148个话题，最终专家们将148个话题中的90个标注为“good”，21个是“intermediate”，37个“bad”。
作者还使评价了好几种度量话题质量的方法。
首先是话题大小，作者将Gibbs抽样候赋给每个话题的单词数量作为话题的大小。图1显示了话题大小和专家度量的话题质量之间的关系。可以看出，话题的大小是可以度量话题质量的。话题越小，质量差的可能性越高。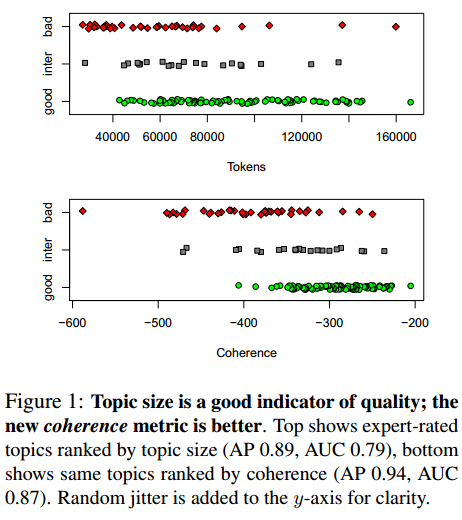
![](http://www.datalearner.com/resources/blog_images/99aa3758-831e-4ca9-beb4-74fe7199728f.png)

##### 话题的一致性指标（Coherence）
但是，这并不是一个最好的办法，据此，作者提出了Coherence的概念来度量话题质量。假设$D(v)$是出现了单词$v$的文档频率，$D(v,v^\*)$表示同事包含单词$v$和单词$v^\*$的文档频率，那么话题的一致性度量如下：
```math
C(t;V^{(t)}) = \sum_{m=2}^{M}\sum_{l=1}^{m-1}\log\frac{D(v_m^{(t)},v_{l}^{(t)})}{D(v_{l}^{(t)})}
```
其中$V^{(t)}$是话题t最有可能前M个单词的列表。
从图1我们也可以看出，话题一致性指标更好的度量了话题的质量。它利用了单词的共现信息。因此，作者认为，标准的LDA模型并没有很好的利用共现信息，据此作者提出了一个新的方法来提高标准LDA的话题质量。

##### 基于Polya's urn的话题模型
作者认为，标准的LDA模型并没有很好的利用词共现的特征，于是作者提出了一个新的话题模型。该模型的document-topic部分与标准LDA模型一致，区别在于抽取话题-词的时候，作者使用了Polya's urn的生成过程。Pólya urn模型是一种统计生成模型，它具有自我加强的属性。举个简单例子，假设某个容器中有黑白两种颜色的球，那么我们随机拿起一个球，根据球的颜色，再放入一个新的相同颜色的球到容器中，原来的球也依然放进去。作者根据这个思想认为，每次抽取话题下的词之后，再根据词共现，将于改词相关的词语再加入到文档中。这样就可以使得具有共现能力的词语更加被容易放到 一个话题中。从而使得某个主题t下的单词w的生成概率为：
```math
P(w|t,W,Z,\beta,A)=\frac{\sum_{v}N_{v|}A_{vw}+\beta}{N_t+|V|\beta}
```
其中A是W×W的实数矩阵，称作外部矩阵。其最简单的形式是单位矩阵。根据作者的评价矩阵，作者把A定义成如下形式：
```math
A_{vv} \propto \lambda_v D(v)
```
```math
A_{vw} \propto \lambda_vD(w,v)
```

赏

支付宝扫码打赏

如果文章对您有帮助，欢迎打赏鼓励作者