高斯混合模型(GMM)
这里主要介绍一下高斯混合模型。这里主要是有限高斯混合模型。
来源1:Douglas Reynolds,MIT Lincoln Laboratory,Gaussian Mixture Models
1、定义
高斯混合模型是一个参数概率密度函数,它是一组高斯密度函数的加权求和。在生物统计领域,高斯混合模型通常是连续测度或者特征的概率分布的参数模型。高斯混合模型可以使用迭代的EM算法或者最大后验概率法估计参数。
2、介绍
高斯混合模型是M个高斯密度的加权求和:
p(x|\lambda)=\sum_{i=1}^{M}w_{i}g(x|\mu_{i},\sum_{i})
其中,$$x$$是$$D$$维连续值数据向量(也就是上面的测度或者是数据),$$w_{i},i=1,..,M$$是混合权重,同时$$g(x|\mu_{i},\sum_{i}),i=1,..,M$$是相应的高斯密度。每一个密度函数是$$D$$元高斯函数的形式:
g(x|\mu_{i},\sum_{i})=\frac{1}{(2\pi)^{D/2}\sum_{i}^{1/2}}\exp[-\frac{1}{2}(x-\mu_{i})'\sum^{-1}_{i}(x-\mu_{i})]
其中,均值向量是$$\mu_{i}$$,协方差矩阵是$$\sum_{i}$$。混合权重需要满足$$\sum_{i=1}^{M}w_{i}=1$$。 完全的高斯混合模型的参数是均值向量,协方差矩阵和所有密度部分的混合权重。这些参数表示如下(公式3):
\lambda=[w_{i},\mu_{i},\sum_{i}],i=1,...,M
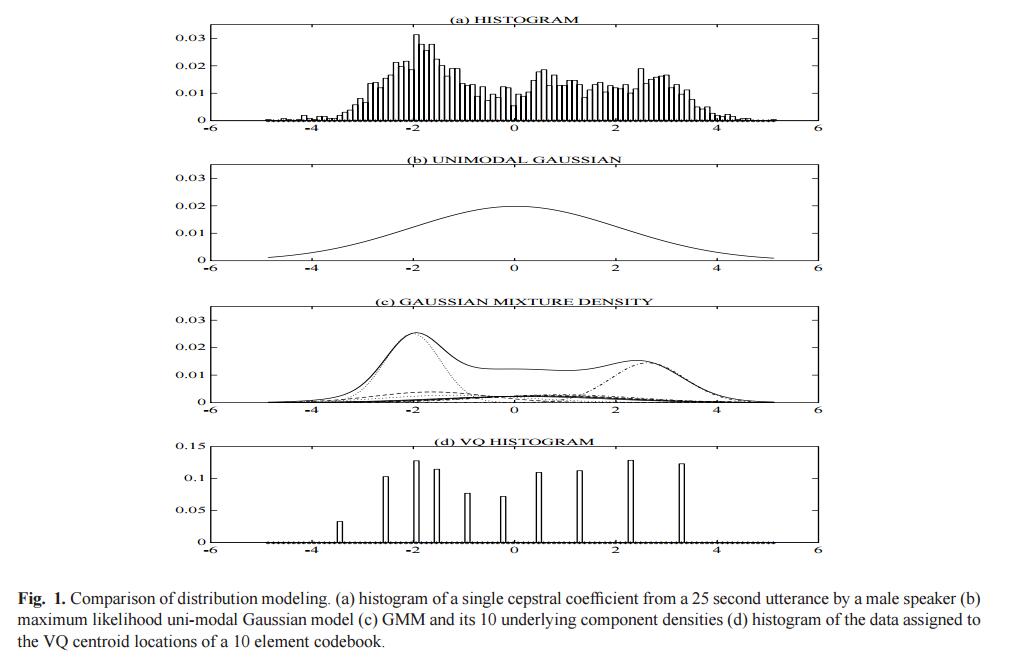
公式3有几个变量。协方差矩阵可以限制为对角矩阵。此外,参数可以在Gaussian成分中被共享因而使所有部分拥有相同的协方差矩阵。模型配置的选择(组件数量,对角协方差矩阵,参数)通常可以根据有效的数据数量确定。 需要知道的是,高斯组成部分是一起为特征密度建模,因此即使特征不是完全统计独立的,完全协方差矩阵(full covariance matrices)并不是必须的。对角协方差的线性组合就可以为特征向量元素建模。使用M个完全协方差矩阵可以被更多的对角协方差代替。 高斯混合模型在生物统计系统中运用广泛,最常见的是会话者识别。高斯混合模型的一个非常好的特性是可以为任意形状的密度函数做近似光滑。传统单峰高斯模型通过一个位置参数(均值向量)、一个椭圆形状参数(协方差矩阵)来为特征分布建模,或者使用一个离散的特征化模板集合,使用矢量量化器(VQ)或者最近邻模型来表示特征分布。而高斯混合模型作为二者的混合,使用了一个离散的高斯函数集合,具有更好的建模能力。图1比较了单峰高斯模型、混合高斯模型和VQ模型的建模情况,图a是一个会话者识别系统的一个特征的直方图。
3、极大似然参数估计
给定训练向量和高斯混合模型的配置,我们希望可以估计GMM的参数,$$\lambda$$,从某种方面讲,就是寻找模型和训练特征向量的最佳匹配结果。估计GMM参数的方法有很多,最有名的是极大似然估计。极大似然估计的目标是寻找模型参数,使得给定训练集条件下,模型的似然率最大。对于给定的一个T序列的训练向量$$X=[x_{1},..,x_{T}]$$,假设向量之间相互独立,那么GMM的似然函数是:
p(X|\lambda)=\prod_{t=1}^{T}p(x_{t}|\lambda)
很不幸,这个表达式不是线性的,因此无法直接获得最大值。然而,极大似然的参数可以使用EM算法求得。 EM算法的基本思想是,初始化一个模型$$\lambda$$,然后用来估计新的模型$$\lambda$$,使得$$p(X|\bar{\lambda})\ge p(X|\lambda)$$。新的模型变成下一次估计的初始模型,迭代直到满足收敛条件。初始模型可以使用VQ估计的一些形式来推导。在EM每一次迭代中,用如下的估计式来确保模型似然值的增长。 混合权重
\bar{w}_{i}=\frac{1}{T}\sum_{t=1}^{T}Pr(i|x_{t},\lambda)
均值
\mu = \frac{\sum_{t=1}^{T}Pr(i|x_{t},\lambda)x_{t}}{\sum_{t=1}^{T}Pr(i|x_{t},\lambda)}
方差(对角协方差)
\bar{\sigma}^{2}_{i} = \frac{\sum_{t=1}^{T}Pr(i|x_{t},\lambda)x_{t}^{2}}{\sum_{t=1}^{T}Pr(i|x_{t},\lambda)}-\bar{\mu}^{2}_{i}
其中,$$\sigma_{i}^{2},x_{t}$$和$$\mu_{i}$$表示相应向量中的任意值。 组成部分i的后延概率为:
Pr(i|x_{t},\lambda) = \frac{w_{i}g(x_{t}|\mu_{i},\sum_{i})}{\sum_{k=1}^{M}w_{k}g(x_{t}|\mu_{k},\sum_{k})}
4、一个实际例子
#从数据中读取样本
x <- read.table("d:/test")$V1
n = length(x)
# breakseq <- seq(100,2000,1)
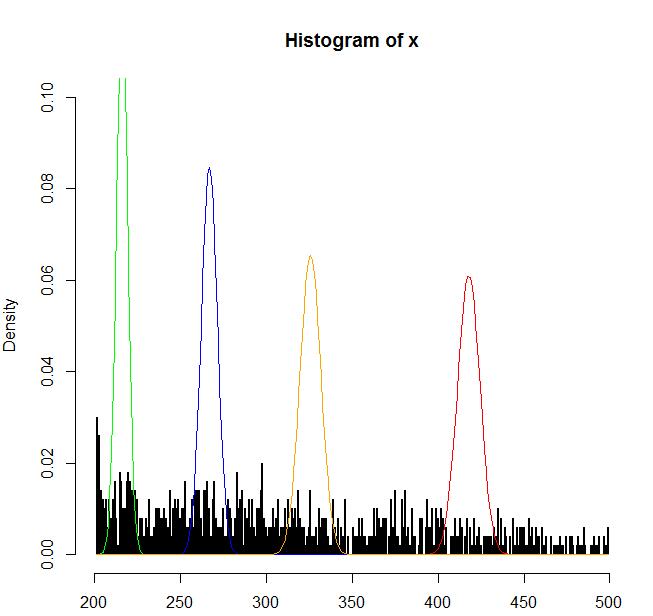
hist(x,breaks=1000,freq=F,ylim=c(0,0.1))
mean(x)
sd(x)
dnorm(2,mean(x),sd(x))
m <- 4 #设置模型数量
miu = runif(m,mean(x)-100,mean(x)+m) #初始化均值
sigma = runif(m,sd(x)^2-100,sd(x)^2+m) #初始化方差
alpha = c(0.2,0.4,0.1,0.3) #初始化alpha
prob = matrix(rep(500,n*m),ncol=m)#初始化协方差
stopValue = 0.00001 #停止条件
#循环EM算法
for(step in 1:1000){
#E步骤
for( j in 1:m ){
prob[,j] <- sapply(x,dnorm,miu[j],sigma[j])
}
probSum <- rowSums(prob)
prob <- prob/probSum
miu_old <- miu
sigma_old <- sigma
alpha_old <- alpha
#M步骤
for(j in 1:m){
p1 <- sum(prob[,j])
p2 <- sum(prob[,j]*x)
p3 <- sum(prob[,j]*(x^2))
miu[j] <- p2/p1
sigma[j] <- sqrt(p3/p1-miu[j]^2)
alpha[j] <- p1/n
}
if( sum(abs(miu-miu_old)) < stopValue &
sum(abs(sigma-sigma_old)) < stopValue &
sum(abs(alpha-alpha_old)) < stopValue ) break
cat('step:',step,'miu:',miu,'sigma:',sigma,'alpha:',alpha,'\n')
}
z<-sort(x)
lines(z,dnorm(z,miu[1],sqrt(sigma[1])),col='red')
lines(z,dnorm(z,miu[2],sqrt(sigma[2])),col='green')
lines(z,dnorm(z,miu[3],sqrt(sigma[3])),col='blue')
lines(z,dnorm(z,miu[4],sqrt(sigma[4])),col='orange')