Dirichlet Distribution（狄利克雷分布）与Dirichlet Process（狄利克雷过程）
103,648 阅读
加载中...
加载中...
欢迎关注 DataLearner 官方微信，获得最新 AI 技术推送
Dirichlet Distribution（狄利克雷分布）与Dirichlet Process（狄利克雷过程）在贝叶斯模型中具有广泛的作用，然而新手对现有的很多材料理解起来可能较为困难，因此我们希望这篇博客能讲清楚相关概念。强烈推荐徐亦达老师在优酷的视频，讲的很清楚，这里我们也借助各种材料来说明一下。 Dirichlet Process（狄利克雷过程）是一个随机过程，在非参数贝叶斯模型中有广泛运用，最常见的是作为混合模型的先验。它是一个分布的分布，Dirichlet过程每次样本的抽取都是一个分布。它被称为Dirichlet过程是因为它在有限维上的边缘分布是Dirichlet分布。像高斯分布一样（这是另一个有名的随机过程，用在贝叶斯回归中，可参考机器学习中的高斯过程），它的有限维边缘分布是高斯分布。从Dirichlet过程中抽取的分布是离散的，但无法使用有限个参数描述，因此它被归为非参数模型。 一个简单的例子 我们知道，在混合模型中，我们假设有观测量$$\{x_1,x_2,...,x_n\}$$，它们分别来自参数为$$\{\theta_i|i=1,2,...,n\}$$的分布（注意每个数据点来自一个分布，其参数为$$\theta$$，那么同一个分布的参数是一样的，也就是说必然存在很多$$\theta$$是相等的）。在贝叶斯方法中，我们需要假设这n个$$\theta$$是来自于某个分布中。注意，如果我们假设$$\theta$$是来自一个连续的分布，也就是说模型的先验分布假设是一个连续分布的话，那么没有哪两个$$\theta$$的值是一样的。因为连续分布的样本不可能有一样的。这显然不符合混合模型的要求。如何解决这个问题呢？我们可以使用Dirichlet Process（狄利克雷过程）作为先验解决这个问题。假设，$$\theta \sim H$$，H可以是连续分布，也可以不是。那么我们可以考虑构造一个离散的分布$$G$$，使$$\theta$$来自于$$G$$来解决这个问题。那么这里我们肯定需要使$$G$$和$$H$$很相似，这样我们才能使用$$G$$中抽取的$$\theta$$。在这里，我们可以定义$$G$$是来自基分布为$$H$$的Dirichlet Process（狄利克雷过程）来解决这个问题。 在说明Dirichlet Process（狄利克雷过程）之前，我们需要了解一下Dirichlet Distribution（狄利克雷分布），它是Beta分布在多元上的推广，其参数是一个实数向量（比如m个$$\alpha$$），它的一个样本就是一个多元向量（比如m个$$\theta$$），它是多项式分布的共轭先验。这篇博客将首先简要介绍一下贝叶斯非参数模型，然后介绍Dirichlet Distribution（狄利克雷分布），接下来将重点说明Dirichlet Process（狄利克雷过程）及其应用。理解Dirichlet Process（狄利克雷过程）需要我们了解测度（measure）的基本概念，因此我们在第三小节中将简要介绍一下这个概念。
目录
概率模型被用在机器学习中为数据建立分布模型。当模型复杂度和有效数据量之间不匹配的时候，传统的参数模型使用固定的和有限维度的参数容易产生过拟合或者不拟合的情况。因此，在参数化模型建模时，在适当的复杂度下进行模型选择是非常重要的问题。然而，不管我们是使用交叉验证，还是使用边缘概率，模型选择都面临很多问题。而非参数贝叶斯模型不需要限制模型的复杂性，因此会缓解不拟合情况，同时通过计算参数的全部的后验概率可以减缓过拟合的情况（个人认为解决过过拟合还是因为层次模型的结构）。
通常，我们都假设我们希望从数据中推断一个潜在的未知的分布。假设$$x_{i}\sim F$$是来自同一个分布且相互独立的样本，其中$$F$$是未知的分布。贝叶斯方法解决这个问题时，会在在计算数据条件下$$F$$后验条件概率给$$F$$一个先验。传统环境下，这个先验会限制在一个范围内，指定参数的范围。而非参数贝叶斯会将这个先验放在一个分布空间中，以获取更好的结果。通常，这个分布空间是所有分布的集合。因此，如此大的选择范围会使后验概率的计算比较麻烦。目前，Dirichlet Process是最流行的贝叶斯非参数模型。
首先，我们给出Dirichlet Distribution（狄利克雷分布）的定义。假设$$\Theta=\{\theta_{1},...,\theta_{m}\}$$ 对Dirichlet分布我们有如下写法：
\Theta \sim Dir(\alpha_{1},...,\alpha_{m})
P(\theta_{1},...,\theta_{m})=\frac{\Gamma(\sum_{k}\alpha_{k})}{\prod_{k}\Gamma(\alpha_{k})}\prod_{k=1}^{m}\theta_{k}^{\alpha_{k}-1}
Dirichlet分布是多项式分布的共轭分布，Beta分布是Dirichlet分布的特例，是二元形式。 根据维基百科的定义，Dirichlet分布是一组连续的多元概率分布，其参数是一个正直向量**$$\alpha$$**。Dirichlet分布常常用在贝叶斯分布中作为先验分布存在。Dirichlet分布的无限维扩展就是Dirichlet过程。为了弄清楚Dirichlet分布，我们可以先了解一下Beta分布（如果对Beta分布没兴趣也可以跳过本小节）。
同样的，根据维基百科，beta分布也是一组连续概率分布，其区间在[0,1]上，参数是两个正值。一般用$$\alpha$$和$$\beta$$表示。这两个参数被称为形状参数，一般以随机变量的指数存在，它们控制着分布的形状。beta分布经常用来为随机变量的行为建模，它把随机变量的行为限制在一个有限的长度范围内。贝叶斯推断中，beta分布通常可以作为贝努利（Bernoulli）、二项分布（binomial）、负二项分布（negative binomial）和几何分布（ geometric distributions）的先验概率分布。例如，在贝叶斯分析中，beta分布可以用来描述关注成功率的分布的原始知识，如太空飞船完成任务的概率。beta分布非常适合用于为百分比和比例模型建模。
beta分布的密度函数
f(x;\alpha,\beta)=constant \cdot x^{\alpha-1}\cdot (1-x)^{\beta-1} = \frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}
其中B表示beta函数。我们可以看一个简单的例子（来源《LDA数学八卦》）：假设有个机器可以随机产生[0,1]之间的随机数，机器运行10次，第7大的数是什么，偏离不超过0.01？这个问题的数学化表达如下：
1.$$X_{1},X_{2},...,X_{n} \sim Uniform(0,1),i.i.d.$$ 2.将这n个随机变量排序得到顺序统计量 $$X_{(1)},X_{(2)},...,X_{(n)}$$ 3.问$$X_{(k)}$$的分布是什么？
我们可以假设计算$$X_{k}$$落在$$[x,x+\Delta x]$$区间上的概率：
P(x \leq X_{k} \leq x+\Delta x)=?
我们将区间分成三个部分$$[0,x),[x,x+\Delta x],(x+\Delta x,1]$$。假设只有1个数落在区间$$[x,x+\Delta x]$$内，那么该事件可以表示：
E=\{ X_{1} \in [x,x+\Delta x], X_{i} \in [0,x)] ,X_{j} \in (x+\Delta x,1]\}
其中，$$i=2,...,k,j=k+1,...,n$$
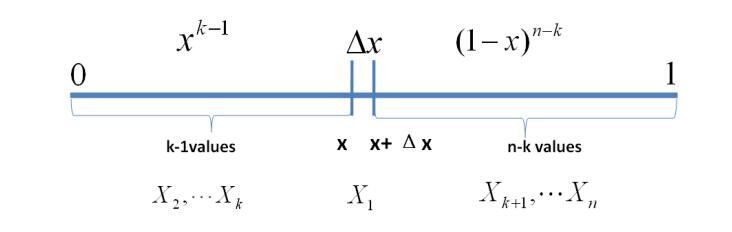
从而有：
P(E)=\prod_{i=1}^{n}P(x_{i})=x^{k-1}(1-x-\Delta x)^{n-k}\Delta x=x^{k-1}(1-x)^{n-k}\Delta x+o(\Delta x)
其中$$o(\Delta x)$$表示$$\Delta x$$的高阶无穷小。根据推断，落在$$[x,x+\Delta x]$$区间的事件超过一个，则对应的事件概率就是$$o(\Delta x)$$。进而我们可以得到$$X_{k}$$的概率密度为：
f(x)=\lim_{\Delta x \to 0}\frac{P(x\leq X_{k}\leq x+\Delta x)}{\Delta x}
= \frac{n!}{(k-1)!(n-k)!}x^{k-1}(1-x)^{n-k}
= \frac{\Gamma(n+1)}{\Gamma(k)\Gamma(n-k+1)}x^{k-1}(1-x)^{n-k}
= \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}
上式即为一般意义上的beta分布，上式在多元上面的推广即为Dirichlet分布。具体的推导过程可以参见《LDA数学八卦》。
beta分布的R语言实例
首先，我们可以画一个beta分布的概率密度函数。
set.seed(1)
x<-seq(0,1,length.out=10000)
plot(0,0,main='probability density function',xlim=c(0,1),ylim=c(0,2.5),ylab='PDF')
lines(x,dbeta(x,0.5,0.5),col='red')
lines(x,dbeta(x,1,2),col='green')
lines(x,dbeta(x,2,2),col='pink')
lines(x,dbeta(x,2,5),col='orange')
lines(x,dbeta(x,1,3),col='blue')
lines(x,dbeta(x,5,1),col='black')
legend('top',legend=c('α=0.5,β=0.5','α=1,β=2','α=2,β=2','α=2,β=5','α=1,β=3','α=5,β=1'),col=c('red','green','pink','orange','blue','black'),lwd=1)
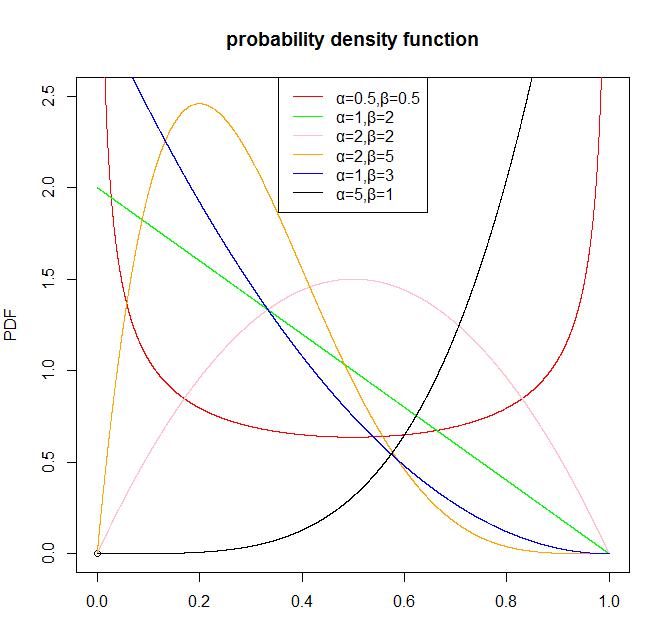
我们再来画一个beta分布的累计概率密度函数
set.seed(1)
x<-seq(0,1,length.out=10000)
plot(0,0,main='cumulative distribution function',xlim=c(0,1),ylim=c(0,1),ylab='PDF')
lines(x,pbeta(x,0.5,0.5),col='red')
lines(x,pbeta(x,1,2),col='green')
lines(x,pbeta(x,2,2),col='pink')
lines(x,pbeta(x,2,5),col='orange')
lines(x,pbeta(x,1,3),col='blue')
lines(x,pbeta(x,5,1),col='black')
legend('topleft',legend=c('α=0.5,β=0.5','α=1,β=2','α=2,β=2','α=2,β=5','α=1,β=3','α=5,β=1'),col=c('red','green','pink','orange','blue','black'),lwd=1)
Dirichelt分布有个非常好的性质，就是聚合性（agglomerative property）。：
(\pi_{1},...,\pi_{K}) \sim Dirichlet(\alpha_{1},...,\alpha_{K})
(\pi_{1}+\pi_{2},\pi_{3},...,\pi_{K}) \sim Dirichlet(\alpha_{1}+\alpha_{2},\alpha_{3},...,\alpha_{K})
一般的，如果$$(l_{1},...,l_{j})$$是$$(1,...,n)$$的一个划分，那么：
(\sum_{i\in l_{1}}\pi_{i},...,\sum_{i \in l_{j}}\pi_{j}) \sim Dirichlet(\sum_{i\in _{1}}\alpha_{i},...,\sum_{i \in l_{j}}\alpha_{j})
聚合性的交叉（converse）也成立：
(\pi_{1},...,\pi_{K}) \sim Dirichlet(\alpha_{1},...,\alpha_{K})
(\tau_{1},\tau_{2}) \sim Dirichlet(\alpha_{1}\beta_{1},\alpha_{1},\beta_{2})
其中，$$\beta_{1}+\beta_{2}=1$$。那么有：
(\pi_{1}\tau_{1},\pi_{1}\tau_{2},\pi_{2},...,\pi_{K}) \sim Dirichlet(\alpha_{1}\beta_{1},\alpha_{1},\beta_{2},\alpha_{2},...,\alpha_{K})
这些性质在Dirichlet过程中也有体现，进而使得相关的模型计算变得非常简单。这里后面会说到。
数学上，测度（Measure）是一个函数，它对一个给定集合的某些子集指定一个数，这个数可以比作大小、体积、概率等等。传统上，积分是针对于区间或者说是连续区间的概念（即我们平时学习的黎曼积分）而言的，测度的概念扩展了集合的概念，也就是产生了勒贝格积分（将积分扩展到任意可测度空间）。测度也可以理解为一个分布函数，它可以将一组数据对应到一个分布上。在Dirichlet Process（狄利克雷过程）中，基分布可以被认为是某些参数空间$$\Theta$$的一个测度，这可以理解成一个分布，就是将该参数空间中某些参数对应到这个分布上，这个分布函数可以理解为这个测度$$H$$。通俗的解释就是，Dirichlet分布是关于某些参数的函数，而在Dirichlet过程中，这些参数变成了函数（因为我们要抽取的样本不再是一个个的实数值，而是一个个的分布）。于是我们就得到了一个关于这些函数的函数，即是关于某些分布的一个分布。因为，在非参数贝叶斯中，假设我们的分布是无数种可能的组合，使用Dirichlet作为这些分布的分布，就可以使我们抽取这些分布的样本了。
前面我们已经说过Dirichlet分布形式如下（它是一组参数空间上的分布）：
\Theta \sim Dir(\alpha_{1},...,\alpha_{m})
P(\theta_{1},...,\theta_{m})=\frac{\Gamma(\sum_{k}\alpha_{k})}{\prod_{k}\Gamma(\alpha_{k})}\prod_{k=1}^{m}\theta_{k}^{\alpha_{k}-1}
在介绍Dirichlet Process之前，我们先说明一下它的应用场景，假设我们有一组数据$ x = \{ x_1,x_2,... \}$，一般情况下，我们都会假设这组数据是来自于参数为$\theta$的分布$x_i|\theta \sim F(\cdot|\theta)$，为了估计这个分布的参数$\theta$，我们一般是给定$\theta$一个先验，然后根据贝叶斯公式写出$\theta$的后验，然后使用极大似然或者极大后验方法估计结果即可。但是，事实上这些数据可能是来自于不同参数的分布，并不是所有的数据都是来自于相同$\theta$下的某个分布。但是有多少个这样的分布我们不知道，总体上来说应该是有无数个这样的分布存在。那么应当如何做呢？我们可以假设这些数据是来自于某些分布$F$，而这些分布不一定相同，并且是来自于无数种可能的分布集合，因此可以给这些分布一个先验，假设这些分布来自于某一组分布，即$F \sim $某些分布划分集合，然后使用上述相似的参数估计方法求出来这些分布（注意到，前者我们是给参数$\theta$一个先验，后者我们是给分布函数一个先验），就能达到我们的目标了。这里某些分布划分集合就是使用Dirichlet Process实现的。
下面我们给出Dirichlet Process的数学描述，并尝试从不同角度去理解。首先我们将Dirichlet分布形式推广到分布上（就是把Dirichlet分布中参数换成某个分布），就可以得到Dirichlet过程：
G \sim DP(\alpha,H)
其中$$\alpha$$是正的尺度参数，$$H$$是基分布。对比Dirichlet分布和Dirichlet过程我们可以发现，前者是对参数空间的分布，后者是对基分布的分布。前者扩展到无限维度即可得到后者。我们可以这样理解二者之间的关系，Dirichlet分布中的样本是一个多项式分布的参数，它可以表征一个多项式，从这个多项式中获取一个样本，通常就是一个多项式抽取的结果了。而Dirichlet过程的一个样本则是关于基分布$H$的一种空间划分，从这个空间划分中抽取一个样本那就是一种分布了。用掷骰子的方式类比就是，前者过程为：假设我们有很多个多面的骰子，每个面向上的概率不一样，我们抽取一个最终样本的过程应该是，首先从很多个骰子中抽取一个骰子（Dirichlet分布抽样），然后掷这个骰子，这个骰子的那个面向上，那么我们就得到这样一个样本。而后者的过程是：假设我们有无数个袋子，每个袋子都有无数多个骰子，Dirichlet过程抽样应该是从这么多袋子中选择一个，然后选择骰子的过程。
Dirichlet过程是一个随机过程，其样本轨道是概率测度。随机过程是函数空间的分布，其样本轨道是从分布中抽取的随机函数。在DP中，就是概率测度的分布，概率测度有一些特殊的属性可以用来当作分布进行推断。因此，从DP中抽取样本可以理解成抽取随机分布。
这里的$$H$$就是之前的分布，在Dirichlet Process（狄利克雷过程）中叫基分布（base distribution）。$$\alpha$$是一个大于0的值，它决定了G有多离散。当$$\alpha=0$$的时候，G就是一个离散的值，当$$\alpha \to \infty$$时，$$G$$和$$H$$就是一样的了。从Dirichlet Process（狄利克雷过程）中抽取的样本是一个完整的分布，它可以理解成是一个测度空间的某种划分结果（也就是说混合模型中划分成几个部分，每个部分是什么样的一个结果）。这里我们就可以明白Dirichlet Process（狄利克雷过程）的作用了，下面我们从不同的角度来说明这个过程的本身情况。
前面已经说过了，DP是一个概率测度上的分布，其样本是一个分布。任意一个DP中的随机分布$$G$$，它的边缘分布必须是Dirichlet分布。特别地，假设$$H$$是参数空间$$\Theta$$上分布，$$\alpha$$是一个正值。对于$$\Theta$$上任意一个有限的测度划分$$A_{1},...,A_{r}$$，因为$$G$$是任意的，向量$$(G(A_{1}),...,G(A_{r}))$$也是任意的。我们说，$$G$$是基分布（base distribution）为$$H$$，集中参数（concentration parameter）是$$\alpha$$的Dirichlet过程，写成$$G \sim DP(\alpha,H)$$，当：
(G(A_{1}),...,G(A_{r})) \sim Dir(\alpha H(A_{1}),...,\alpha H(A_{r}))
其中$$A_{1},...,A_{r}$$是参数空间$$\Theta$$的任意一个有限划分。这就是从集合划分的角度理解DP。
我们说过，DP是一个关于分布的分布，其最重要的作用是作为数据所属的分布的先验存在。既然是分布就可以抽样（尽管其样本是一个分布）。假设有：
G \sim \textbf{DP}(\alpha,H)
X_n|G \sim G \space\space\space\space \textbf{for}\space n=\{1,...,N\}
直接抽取分布显然是不可能的。但是，在这里我们假设某个数据X是来自一个分布G，而这个分布是来自于某个DP，即其先验是个DP。那么就有上述两步。在积分掉G之后，我们就可以得出样本的联合分布了。
P(X_1,...,X_N) = \int P(G)\prod_{n=1}^NP(X_n|G)dG
假设这些数据样本都是有顺序的，我们对已经存在了n-1个观测值的情况下，下一个样本$X_n$的来源很感兴趣，那么我们就有:
X_n|X_1,...,X_{n-1} =
\begin{cases}
X_i \space\space\space\space \textbf{with probability} \frac{1}{n-1+\alpha}\\
\textbf{new draw from H} \space\space\space\space \textbf{with probability} \frac{\alpha}{n-1+\alpha}
\end{cases}
假设这些观测值最终只是来自于K种分布：
X_k^{*} \space\textbf{for}\space k\in\{1,...,K\}
在我们给正式的定义之前，我们先把DP当作一个无限维Dirichlet分布的生成过程来做一个解释。考虑贝叶斯混合模型，有K个部分组成：
\pi|\alpha \sim Dir(\frac{\alpha}{K},...,\frac{\alpha}{K})
z_{i}|\pi \sim Mult(\pi)
\theta_{k}^{*}|H \sim H
x_{i}|z_{i},\{\theta_{k}^{*}\} \sim F(\theta^{*}_{z_{i}})
其中，$$\pi$$是混合属性，$$\alpha$$是Dirichlet先验的伪计数超参数（关于为什么叫伪计数可以参考《LDA数学八卦》），$$H$$是组件参数$$\theta^{*}_{k}$$的先验，$$F(\theta)$$是组件分布，其参数是$$\theta$$（组件就是指混合分布中的一个部分，英文是component，中文翻译应该是组成部分，但没找到合适的词）。可以看到，当$$K$$很大的时候，由于我们以特殊的方法设置$$\pi$$的参数先验，用来为$$n$$个数据点建模的组件的数量K是独立的，并大约等于$$O(\alpha\log n)$$。这意味着$$K\to \infty$$时，模型会保持稳定，从而会产生无限混合模型。这个模型最早提出来用于确定混合问题中组件数量。现在这个模型被称为DPMM。 这里也可以看出Dirichelt分布与Dirichlet过程之间的联系。Dirichlet分布是参数空间$$\Theta$$的参数$$\theta_{1},...,\theta_{m}$$服从Dirichlet分布，我们关心的是参数的分布。而Dirichlet过程是基于这些参数的分布$$G(A_1),...,G(A_r)$$服从Dirichlet分布，我们关心是参数空间上分布的分布。 参数$$H$$和$$\alpha$$是DP定义中非常直观的角色。基分布可以理解成DP的均值（即Dirichlet过程从基分布附近抽取分布，就像高斯分布从均值附近抽取样本一样）。尽管基分布是连续的，但Dirichlet抽取的分布却是离散的。集中参数表明了离散化的程度：当$$\alpha \to 0$$时，Dirichlet过程的实现结果趋向于一个值，当$$\alpha \to \infty$$时，其结果就变成了连续的了。介于二者之间就是离散的结果。对于任意一个测度集合$$A \subset \Theta$$，我们有
E[G(A)]=H(A)
另一方面，集中参数可以被当作逆方差（inverse variance）：
V[G(A)]=\frac{H(A)(1-H(A))}{(\alpha+1)}
当$$\alpha$$越大的时候，方差越小，DP的质量就会更加集中分布在其均值附近。集中参数也称为力量参数，表示当使用DP作为贝叶斯非参数模型中的分布的非参数先验的时候，先验的力量。它也被称为质量参数，因为这个先验的力量可以通过观测量样本大小来衡量。同时，注意到，$$\alpha$$和$$H$$只作为乘积在公式2中出现。因此有些作者定义$$\tilde{H}=\alpha H$$作为DP的单参数，因此用$$DP(\tilde{H})$$代替$$DP(\alpha,H)$$。这种表示方法非常简便，但却丢失了$$\alpha$$和$$H$$不同的含义。
由于$$\alpha$$表示DP的均值集中程度，因此，当$$\alpha \to \infty$$时，我们有$$G(A)\to H(A)$$。但是，这并不是说$$G\to H$$。后面我们会看到，即使$$H$$是光滑的，我们从$$DP$$中抽取出来的样本也是离散的分布。因此，$$G$$和$$H$$甚至都不需要是绝对连续的。但是，当我们需要关注光滑性的时候，可以通过把$$G$$变成核函数来使得结果的随机分布拥有密度函数。
这里有个相关的问题是参数空间$$\Theta$$的所有可能的分布下DP的覆盖范围。我们已经知道DP的样本是离散的，因此DP下的分布集合大小比较小。但实际上不是这样，如果H是所有的可能集合，那么$$\Theta$$下任意分布都可以近似成为DP的任意序列。
在最简单的概率空间中，测度划分的数量都非常大。一个很自然的问题是，目标是否满足这样大规模的条件。这里有一堆文献解释，我没看原文献就暂时不翻译了。
######3.2.4 让我们从无限混合模型的角度再来理解一下Dirichlet过程。 一个有限的混合模型定义如下：
\theta_{k}^{*} \sim H
\pi \sim Dir(\frac{\alpha}{K},...,\frac{\alpha}{K})
z_{i}|\pi \sim Mult(\pi)
x_{i}|\theta_{z_{i}}^{*} \sim F(\cdot|\theta^{*}_{z_{i}})
这个模型的参数有 1. H中的超参数 2. Dirichlet参数$$\alpha$$ 3. 模型的个数K（确定K的值是最困难的） 假设$$K\gg0$$非常大。那么如果参数$$\theta_{k}^{*}$$和混合比例$$\pi$$可以被积分掉，潜在变量的个数并不随着K的增长而增加。那么数据最多只有n个“活跃”(active)部分。实际上，“活跃”部分远远小于n。这就是无限混合模型。
假设$$G \sim DP(\alpha,H)$$。由于$$G$$是一个分布，我们可以从$$G$$中抽取样本。假设$$\theta_{1},...,\theta_{n}$$是从$$G$$中抽取的独立序列。注意到$$\theta_{i}$$的取值实在$$\Theta$$中，因为$$G$$是$$\Theta$$上的分布。我们比较感兴趣的是在给定$$\theta_{1},...,\theta_{n}$$的观测值条件下，$$G$$的后验分布。假设$$A_{1},...,A_{r}$$是$$\Theta$$的一个有限测度划分，$$n_{k}=\#\{i:\theta_{i}\in A_{k}\}$$是$$A_{k}$$观测值的数量。我们有：
(G(A_{1}),...,G(A_{r}))|\theta_{1},...,\theta_{n} \sim Dir(\alpha H(A_{1})+n_{1},...,\alpha H(A_{1})+n_{r})
由于上式在所有有限测度划分中都成立，那么$$G$$的后验分布一定也是一个Dirichlet过程。有点代数知识都可以看出来，后验DP把集中参数变成了$$\alpha+n$$，基分布则变成了$$\frac{\alpha H+\sum_{i=1}^{n}\delta_{\theta_{i}}}{\alpha+n}$$，其中，$$\delta_{i}$$是$$\theta_{i}$$位置上的点质量，同时，$$n_{k}=\sum_{i=1}^{n}\delta_{i}(A_{k})$$。换句话说，DP提供了一个先验分布簇，针对那些在观测值下与后验很接近的分布（In other words, the DP provides a conjugate family of priors over distributions that is closed under posterior updates given observations.）把后验DP重新写一下，我们就可以得到
G|\theta_{1},...,\theta_{n} \sim DP(\alpha+n,\frac{\alpha}{\alpha+n}H+\frac{n}{\alpha+n}\frac{\sum_{i=1}^{n}\delta_{\theta_{i}}}{n})
注意到，后验基分布是先验分布$$H$$和实际分布$$\frac{\sum_{i=1}^{n}\delta_{\theta_{i}}}{n}$$的加权和。先验的权重与$$\alpha$$成正比，实际分布的权重和观测值数量$$n$$成正比。因此，我们可以把$$\alpha$$称为先验的质量或者力量。Dirichlet过程的后验依然是一个Dirichlet过程。
首先我们回一下用Dirichlet过程进行密度估计，假设：
G \sim DP(\alpha,H)
x_{i} \sim G
我们想估计上面的$$x_{i}$$的密度函数，但不可以。原因是Dirichelt过程是一个离散的分布，因此，它没有密度函数。为了解决这个问题我们可以将DP进行平滑：
G \sim DP(\alpha,H)
F(\cdot) = \int F(\cdot|\theta)dG(\theta)
x_{i} \sim F_{x}
上面的内容可以转化成
G = \sum_{k=1}^{\infty}\pi_{k}\delta_{\theta^{*}_{k}}
F(\cdot) = \sum_{k=1}^{\infty} \pi_{k} F(\cdot|\theta_{K}^{*})
x_{i} \sim F_{x}
我们接着来看上面小节说的密度估计公式：
G = \sum_{k=1}^{\infty}\pi_{k}\delta_{\theta^{*}_{k}}
F(\cdot) = \sum_{k=1}^{\infty} \pi_{k} F(\cdot|\theta_{K}^{*})
x_{i} \sim F_{x}
这个公式可以换种写法：
z_{i} \sim Discrete(\pi)
\theta_{i} = \theta^{*}_{z_{i}}
x_{i}|z_{i} \sim F(\cdot|\theta_{i})=F(\cdot|\theta_{z_{i}^{*}})
这就是一个非常简单的无线混合模型，称为Drichilet过程混合模型（Dirichlet Process Mixture Model，DPMM）。Dirichlet 过程混合模型在很多聚类应用中都存在，当我们认为簇的数量并不知道且不会随着数据的增加有限制的时候，我们就可以使用DPMM。 DP不仅仅可以用于聚类，也可以用在潜在对象未知或者没有限制的情况下：
相关的问题，如群组聚类（grouped clustering）可以使用层次Dirichlet过程（hierarchical Dirichlet Process）解决。
这里我们只给出简单的形式：
G_{0}|\gamma,H \sim DP(\gamma,H)
G_{j}|\alpha,G_{0} \sim DP(\alpha,G_{0})
\theta_{ji}|G_{j}=G_{j}
来源1：Dirichlet Process : Tutorial and Practical Course，Yee Whye Teh 来源2：Dirichlet Processes：A gentle tutorial， Khalid El-Arini 来源3：https://en.wikipedia.org/wiki/Dirichlet_distribution 来源4：https://en.wikipedia.org/wiki/Beta_distribution 来源5：LDA 数学八卦，靳志辉 来源6：Dirichelt Process：徐亦达的优酷视频：http://i.youku.com/i/UMzIzNDgxNTg5Ng==