多元高斯分布（多元正态分布）简介

高斯分布（Gaussian Distribution），也称作是正态分布（Normal Distribution），是一种非常常见的分布，对于一元高斯分布（Univariate Gaussian Distribution）我们比较熟悉，对于高斯分布的多元形式有很多人不太理解。我们将简单介绍一下多元高斯分布的相关性质。这篇博客的材料主要来源Andrew Ng在斯坦福机器学习课的材料。[[1]][1] [1]: http://cs229.stanford.edu/materials.html "斯坦福机器学习课程材料"

多元高斯分布（Multivariate Gaussian Distribution）的形式很简单，就是一元高斯分布的在向量形式的推广。我们把向量$X=[X_1,X_2,...,X_n]^T$称作是均值为$\mu \in \bold{R}^n$，协方差矩阵为$\Sigma \in S^n$的多元高斯分布，如果它具有如下概率密度函数的形式：

p(x;\mu , \Sigma)=\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))

#### 一、多元高斯分布与一元高斯分布的关系 首先，我们回顾一下一元正态分布的形式，其概率密度函数如下： ```math p(x;\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{1}{2\sigma^2}(x-\mu)^2) ``` 这里指数函数的参数$(-\frac{1}{2\sigma^2}(x-\mu)^2)$是一个关于x的二次项式函数。由于二次项的系数为负，因此它是抛物线开口向下的函数。此外，最前面的系数是$\frac{1}{\sqrt{2\pi}\sigma}$是与x无关的形式，因此我们可以把它当做是一个“正规化因子”（normalization factor），以保证： ```math \frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}\exp(-\frac{1}{2\sigma^2}(x-\mu)^2)=1 ``` 在多元高斯密度中，指数函数的参数是$-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)$，其中x是向量。由于$\Sigma$是正定的（positive definite），而任意正定矩阵的逆矩阵也是正定的。那么对于任意一个非零向量z，有$z^T \Sigma z>0$，也就是说对于任意的$x \neq \mu$，有： ```math (x-\mu)^T\Sigma^{-1}(x-\mu) > 0 ``` ```math -\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu) < 0 ``` 与一元高斯分布类似，我们可以把该指数函数的参数当做一个开口向下的二次曲面（downward opening quadratic bowl）。在多元高斯密度函数中，前面的系数的形式比一元高斯分布要复杂很多，但它也同样的不依赖于x。因此，它也是一个正规化系数：

-\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\ldots\int_{-\infty}^{\infty}\exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)) dx_1 dx_2 \ldots dx_n = 1

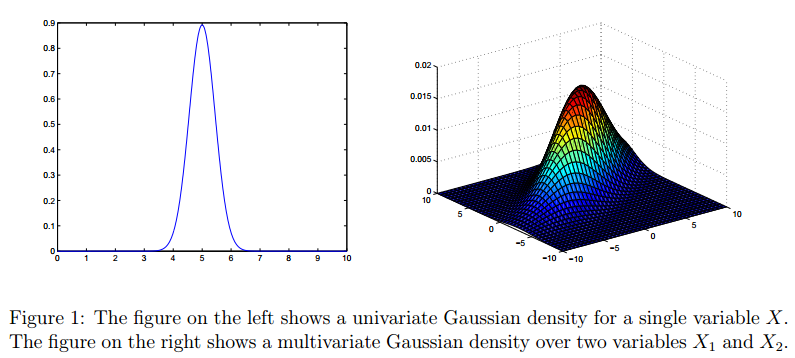
二、协方差矩阵（The covariance matrix）

协方差矩阵的概念对理解多元高斯分布来说非常重要。回忆一下，对于一对随机变量X和Y，它们的协方差矩阵定义如下：

Cov[X,Y]=E[(X-E[X])(Y-E[Y])]=E[XY]-E[X]E[Y]

对于多个变量来说，协方差矩阵是一个非常简洁的表达变量关系的方式。通常，我们用$\Sigma$表示协方差矩阵，它是一个$n \times n$的矩阵，其中第$(i,j)$的位置表示$Cov[X_i,X_j]$。下面还有一些命题，可以帮助我们理解一个随机向量X的协方差矩阵。

**命题1：**对于任意一个随机向量X，其均值为$\mu$，协方差为$\Sigma$，我们有：

\Sigma = E[(X-\mu)(X-\mu)^T]=E[XX^T]-\mu\mu^T

在多元高斯分布的定义中，我们要求协方差矩阵是一个对称的正定矩阵。为什么有这个限制存在呢？实际上，对于任意的一个随机向量的协方差矩阵，它都是对称的半正定矩阵。

**命题2：**假设$\Sigma$是一个随机向量X的协方差矩阵，那么，$\Sigma$一定是一个对称的半正定矩阵。证明如下：

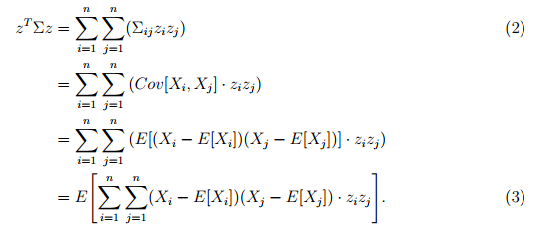
三、对角协方差矩阵的例子

为了直观地理解一个多元高斯分布是什么样的，我们以最简单的n=2为例说明，并且我们假设其协方差矩阵是对角阵：

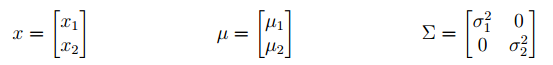
那么，其多元高斯密度函数的形式如下：

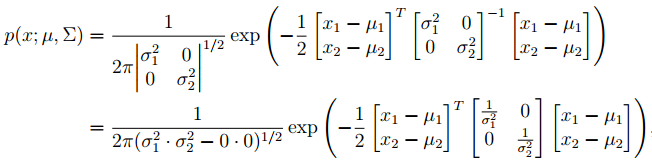
继续：

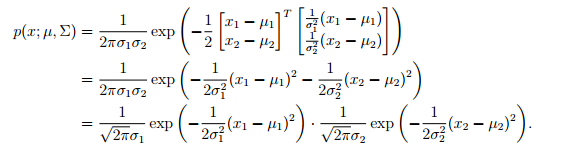
最后一行我们可以看出，这个二元高斯分布的密度函数就是两个独立的高斯密度乘积形式。也就是说，更一般的情况，当协方差矩阵是对角阵的时候，多元高斯分布就是一组相互独立的一元高斯分布的组合。

四、等量线

另一个理解多元高斯分布的方法是从其等量线的形状来看。对于一个函数$f:R^2 \to R$，其等量线是如下形式的集合：

{x \in R^2 : f(x)=c}

4.1 等量线的形状

一个多元高斯分布的等量线是什么样的？我们依然以前面的二元对角协方差矩阵为例。让我们考虑某些常量情况下的等量线：

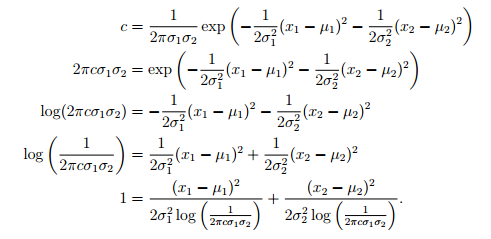
我们可以定义：

那么，它服从：

1=(\frac{x_1-\mu}{r_1})^2+(\frac{x_2-\mu}{r_2})^2

这个形式应该比较熟悉了，就是高中解析几何里面的轴对称的椭圆了。

#####4.2 坐标轴长度 为了更好的理解等量线如何随着多元高斯分布的变化而变化，我们看一下在高斯密度函数的峰值位置，也就是$c=1/e$时，$r_1$和$r_2$的位置。首先我们通过公式4可以看到，当$x_1=\mu_1$且$x_2=\mu_2$到时候，高斯密度是位置最高，为$1/(2\pi\sigma_1\sigma_2)$。 然后，我们把$c=\frac{1}{e}\frac{1}{2\pi\sigma_1\sigma_2}$代入上式，我们有：

从这个地方我们看出，坐标轴长度与标准差$\sigma_i$成一定比例。这样容易理解，如果某些随机变量$x_i$比较小，那么高斯分布在那个维度上的线就越紧密，因此，半径$r_i$就更小。

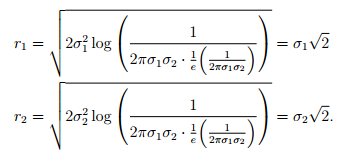
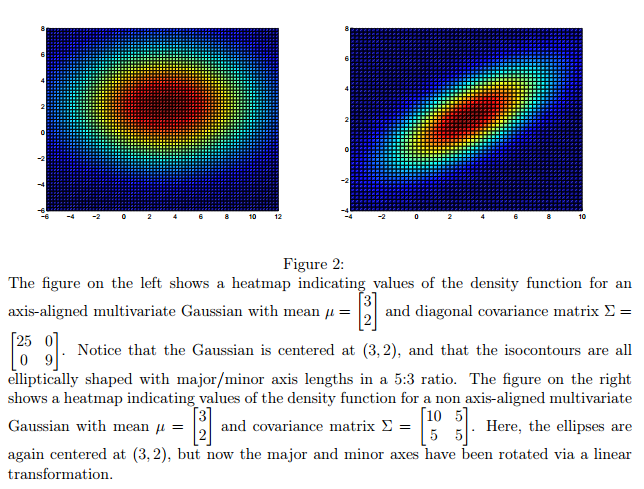
4.3 非对角阵的情况，更高维的情况

显然，上述推到都是依赖于假设$\Sigma$是对角阵。然而，在非对角阵的情况下，图形也是类似的，只是轴对称的椭圆变成了一个变形的椭圆。

五、线性变换的解释 在最后几节里，我们将主要关注拥有对角协方差矩阵的多元高斯分布的一些特性。我们知道，对于对角协方差矩阵，我们可以把一个多元高斯分布看作是n个独立高斯分布的集合。在这里，我们将进一步了解其中的特性。 本节的最关键结果就是下面的理论：

理论1：如果$X\sim N(\mu,\Sigma)$，且其协方差矩阵是对角的正定矩阵，那么一定存在一个矩阵$B \in R^{n \times n}$使我们可以定义$Z=B^{-1}(B-\mu)$，有$Z \sim N(0,I)$。

如何理解这个理论呢？注意到，如果$Z\sim N(0,I)$，那么使用第4节的分析我们可以得到，Z是n个独立标准正太随机变量的集合。也就是，如果$Z=B^{-1}(X-\mu)$，那么，$X=BZ+\mu$。因此，该理论说明，任意多元高斯分布X都可以运用线性变换（$X=BZ+\mu$）把它变成一组n个独立的标准正态分布变量的集合。