平衡二叉树之AVL树（Adelson-Velsky and Landis Tree）简介及Java实现

[toc]

一、AVL树简介

在前面的内容中，我们已经介绍了平衡二叉树。其中提到了AVL树，这是一种非常著名的平衡二叉树。

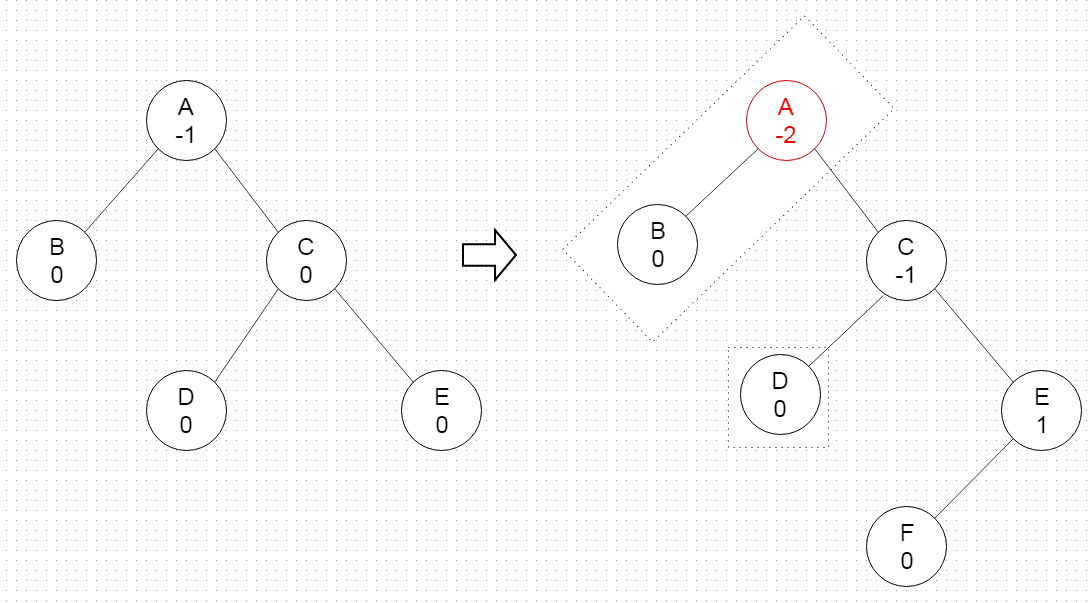
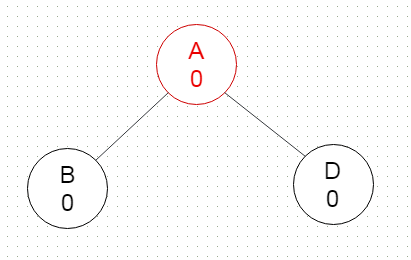
在计算机科学中，AVL树（以发明者Adelson-Velsky和Landis命名）是一种自平衡二叉查找树。这是第一个发明类似自平衡机制的二叉树数据结构。在AVL树中，任何节点的两个子树的高度最多相差一个。如果在任何时候它们相差多于一个，则重新平衡以恢复此属性。查找，插入和删除在平均和最差情况下都需要$O(\log n)$时间，其中n是操作之前树中的节点数。插入和删除可能需要通过一个或多个树旋转来重新平衡树。

AVL树以其两位苏联发明家Georgy Adelson-Velsky和Evgenii Landis命名，他们在1962年的论文“An algorithm for the organization of information”中发表了这篇论文。

AVL树通常与红黑树进行比较，因为它们都支持相同的操作，并且对基本操作都是$O(\log n)$时间。对于查找密集型应用程序，AVL树比红黑树快，因为它们更严格地平衡。与红黑树相似，AVL树是高度平衡树。

二、平衡因子（Balance Factor）

package com.huawei.machinelearning.data.structure; /** * AVL Tree implementation * Created by d00454735 on 2018/10/26. */ public class AVLTree { AVLNode root; // 根节点 // 右旋转 private AVLNode rightRotate(AVLNode rootNode){ AVLNode newRootNode = rootNode.leftNode; // 新的根节点是原来根节点的左节点 // 将新的根节点的右节点拿出来，然后拼到原来的根节点上 AVLNode pruningNode = newRootNode.rightNode; // 再把拼接后的节点放到新根节点的左边 newRootNode.rightNode = rootNode; rootNode.leftNode = pruningNode; // 更新节点高度 updateNodeHeight(rootNode); updateNodeHeight(newRootNode); return newRootNode; // 返回新的根节点 } // 左旋转 private AVLNode leftRotate(AVLNode rootNode){ AVLNode newRootNode = rootNode.rightNode; // 新的根节点是原来根节点的右节点 // 将新的根节点的左节点拿出来，然后拼到原来的根节点上 AVLNode pruningNode = newRootNode.leftNode; // 再把拼接后的节点放到新根节点的左边 newRootNode.leftNode = rootNode; rootNode.rightNode = pruningNode; // 更新节点高度 updateNodeHeight(rootNode); updateNodeHeight(newRootNode); return newRootNode; // 返回新的根节点 } // 插入一个新节点 AVLNode insert(AVLNode avlNode, int key) { // 如果节点为空，当前插入的是根节点 (avlNode == ) { ((key)); } (key < avlNode.key) { avlNode.leftNode = insert(avlNode.leftNode, key); } (key > avlNode.key) { avlNode.rightNode = insert(avlNode.rightNode, key); } { avlNode; } updateNodeHeight(avlNode); getBalance(avlNode); ( balance > && key < avlNode.leftNode.key ){ rightRotate(avlNode); } ( balance < - && key > avlNode.rightNode.key ){ leftRotate(avlNode); } ( balance > && key > avlNode.leftNode.key){ avlNode.leftNode = leftRotate(avlNode.leftNode); rightRotate(avlNode); } ( balance < - && key < avlNode.rightNode.key){ avlNode.rightNode = rightRotate(avlNode.rightNode); leftRotate(avlNode); } avlNode; } { ( avlNode == ){ ; } height(avlNode.leftNode) - height(avlNode.rightNode); } { avlNode.height = max(height(avlNode.leftNode), height(avlNode.rightNode))+; } { h1 > h2 ? h1 : h2; } { ( avlNode == ){ ; } avlNode.height; } { (node != ) { System.out.print(node.key + ); preOrder(node.leftNode); preOrder(node.rightNode); } } { (); tree.root = tree.insert(tree.root, ); tree.root = tree.insert(tree.root, ); tree.root = tree.insert(tree.root, ); tree.root = tree.insert(tree.root, ); tree.root = tree.insert(tree.root, ); tree.root = tree.insert(tree.root, ); System.out.println( + ); tree.preOrder(tree.root); } } { key; height; AVLNode leftNode, rightNode; AVLNode( d) { key = d; height = ; } }

平衡二叉树之AVL树（Adelson-Velsky and Landis Tree）简介及Java实现

一、AVL树简介

二、平衡因子（Balance Factor）

DataLearner 官方微信

三、自平衡适应

四、AVL树的Java实现

热门博客