这是一篇来自Towards Data Science上面的一篇个人实践分享,主要是针对销量进行预测。一般来说,销量受到价格、季节等因素影响较大。这里就是考虑这些因素进行的一个实践。值得大家一试。这里我们翻译一下,并对其中的某些工作做一些简单的解释。
这份工作使用的是Prophet工具,这个工具是Facebook贡献的一个时间序列分析预测工具,对周期的捕获很好,是一个开源的工具。这份实践最大的收获应该包括以下几个:
- 首先是作者在预测之前做了很多数据探索的工作,这些工作对我们来说有很好的启示,这其实是做数据分析或者数据挖掘必不可少的步骤,尽管大多数人这方面并没有投入很多时间。
- 其次是作者在做数据探索的时候使用了seaborn这个工具,这个工具我之前也没有用过,但是发现这真的是做数据探索的很方便的工具。
- 最后是作者有一个非常简单的Prophet使用代码,还包括添加自定义的周期,这个对于入门Prophet来说非常合适。
原文:https://towardsdatascience.com/sales-forecasting-with-price-promotion-effects-b5d70207b128
欢迎关注 DataLearner 官方微信,获得最新 AI 技术推送
一、前言
许多公司的业务是非常季节性的,其中有些在假期期间赚钱,例如超级碗,劳动节,感恩节和圣诞节。 此外,他们在一年中的数周内使用促销手段来增加对产品或服务的需求或可见性。
在这篇文章中,我们将使用时间序列分析技术来分析历史数据,并考虑促销的影响等。
我们将使用的数据是9家商店和3种产品的每周销售和价格数据。 最后,我们将预测其中一家商店的三种产品之一在未来50周内的销售情况。具体的数据可以去这里下载。
二、数据描述
这个数据包含了七列的内容,主要是9个商店的3中商品在过去一段时间的周销量:
- Store:这是商店的ID,总共有9个商店
- Product:这个是产品的ID,总共有3中商品
- Date:这是某一周起始时间
- Is_Holiday:这个表示那一周的是否包含假日(不是周末这种,是指如圣诞节这样的节日)
- Base Price:这个表示没有折扣情况下商品的价格
- Price:这个表示当前周实际的价格
- Weekly_Units_Sold:这个就是周的销量了
import plotly.express as px
from fbprophet import Prophet
from sklearn.metrics import mean_squared_error
from math import sqrt
from statsmodels.distributions.empirical_distribution import ECDF
import datetime
df = pd.read_csv('data/Sales_Product_Price_by_Store.csv')
df['Date'] = pd.to_datetime(df['Date'])
df['weekly_sales'] = df['Price'] * df['Weekly_Units_Sold']
df.set_index('Date', inplace=True)
df['year'] = df.index.year
df['month'] = df.index.month
df['day'] = df.index.day
df['week_of_year'] = df.index.weekofyear
在数据预处理的时候,我们将日期这个特征做了一点预处理,抽取了年份、月份等。注意,这里作者加了一个销售金额的列(weekly_sales),下面要用到,记住。这是很常见的处理方式。
三、探索性数据分析(EDA,Explanatory Data Analysis)
在实际分析之前,我们做一些数据探索。首先,作者画了一个经验分布函数的图(经验分布函数就是样本分布函数,是一个离散型随机变量的分布函数,这个不知道自己去谷歌一下了)。
sns.set(style = "ticks")
c = '#386B7F'
figure, axes = plt.subplots(nrows=2, ncols=2)
figure.tight_layout(pad=2.0)
plt.subplot(211)
cdf = ECDF(df['Weekly_Units_Sold'])
plt.plot(cdf.x, cdf.y, label = "statmodels", color = c);
plt.xlabel('Weekly Units Sold'); plt.ylabel('ECDF');
plt.subplot(212)
cdf = ECDF(df['weekly_sales'])
plt.plot(cdf.x, cdf.y, label = "statmodels", color = c);
plt.xlabel('Weekly sales');
这里作者得出了两个结论(这个是常见的结论了,大多数都应该差不多):
-
尽管在最佳的一周中,一家商店售出了2500多个单位,但大约有80%的时间,每周的销售量不超过500。
-
尽管最高的每周销售额超过了2.5万美元,但超过90%的数据的每周销售额不到5000美元。
然后作者根据商店分组,分别看看各家商店的销售额情况:
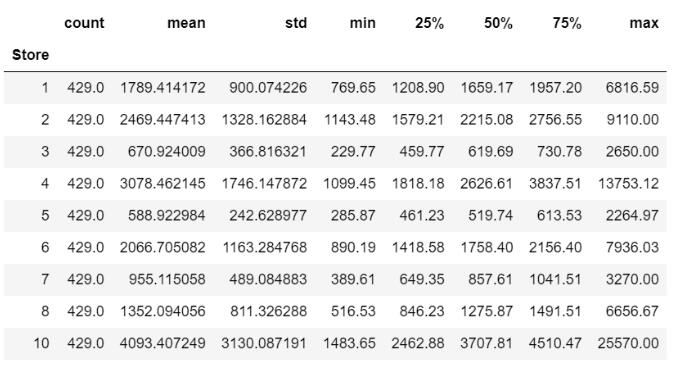
df.groupby('Store')['weekly_sales'].describe()
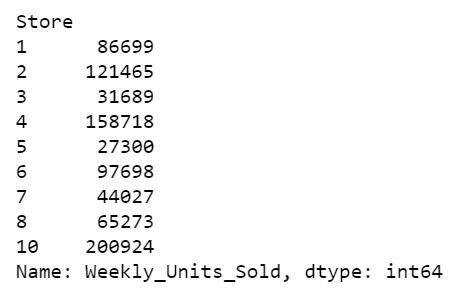
df.groupby('Store')['Weekly_Units_Sold'].sum()
- 显而易见,在所有9家商店中,Store 10的每周平均销售额最高,而Store 10的每周总销售量最高。
- 而商店5的平均每周销售额最低。
- 显然,商店10是最畅销,最拥挤的商店。
再看看不同商品在不同周的销售情况(这里用的是seaborn这个python库,有点意思,看起来比较复杂的展示一句话就能搞定,这个是编程的技巧,重点!):
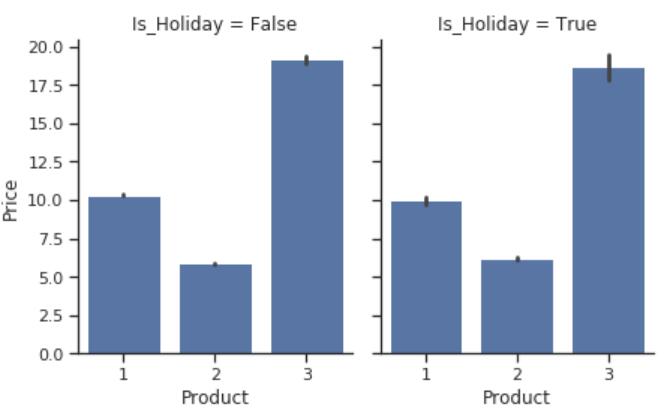
g = sns.FacetGrid(df, col="Is_Holiday", height=4, aspect=.8)
g.map(sns.barplot, "Product", "Price");
简单解释一下,这个FacetGrid函数是用来分片展示的,也就是你指定某些列或者行,它会根据这些列和行自动将数据进行分片,后面分成了几个,就能画出几个结果。这里展示的根据是否是假期分片之后,展示价格与产品的关系,也就是看看假期与非假期时候,商店里面的产品与价格的关系。
接下来作者还看了一下假期与非假期时候,商店里面的产品与销量的关系。
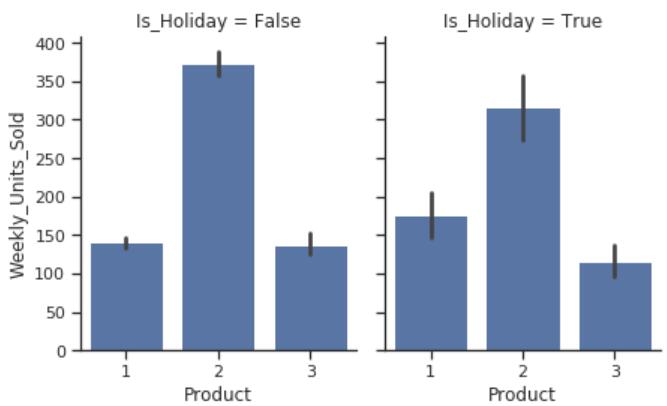
g = sns.FacetGrid(df, col="Is_Holiday", height=4, aspect=.8)
g.map(sns.barplot, "Product", "Weekly_Units_Sold");
- 产品2是所有三种产品中最便宜的产品,并且销量最高。
- 产品3是所有三种产品中最昂贵的产品。
- 另外,假日期间商品价格没有变化。
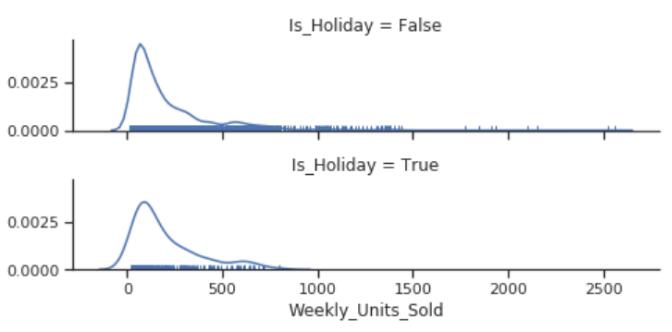
g = sns.FacetGrid(df, row="Is_Holiday",
height=1.7, aspect=4,)
g.map(sns.distplot, "Weekly_Units_Sold", hist=False, rug=True);
再根据商店的情况,看看假期在不同商店之间的销量是否有差别(这里继续用seaborn提供的函数,话说这个库真的是方便)。
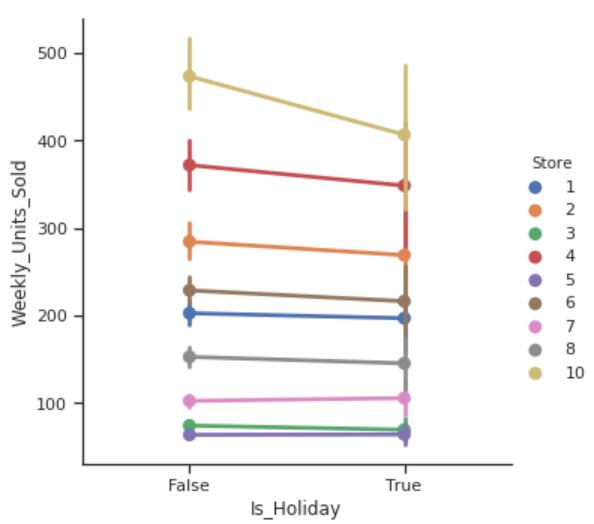
sns.factorplot(data= df,
x= 'Is_Holiday',
y= 'Weekly_Units_Sold',
hue= 'Store');
这里的factorplot是用来分析数值变量与类别变量之间的关系的,画的是箱线图,这个图很有名,不会自己谷歌了。结果如下:
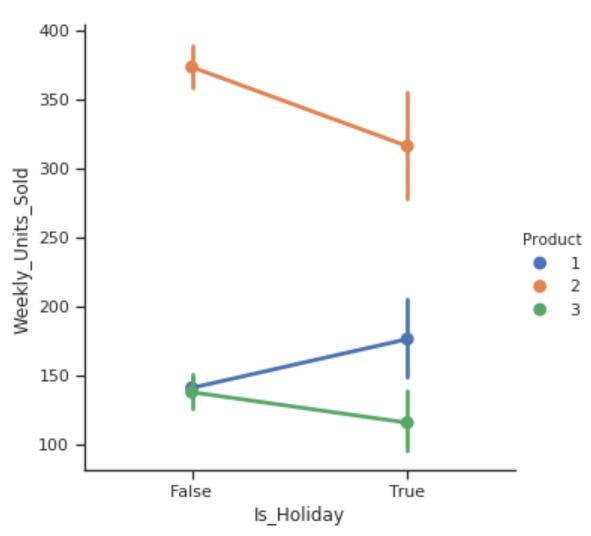
sns.factorplot(data= df,
x= 'Is_Holiday',
y= 'Weekly_Units_Sold',
hue= 'Product');
- 假期似乎对企业没有积极影响。 对于大多数商店,假日期间每周的销售量与正常天相同,而商店10在假日期间有所减少。
- 在假期期间,产品1的周销售量略有增加,而产品2和产品3的周期间减少。
接下来继续看看不同产品具体的价格与销量的关系分布情况
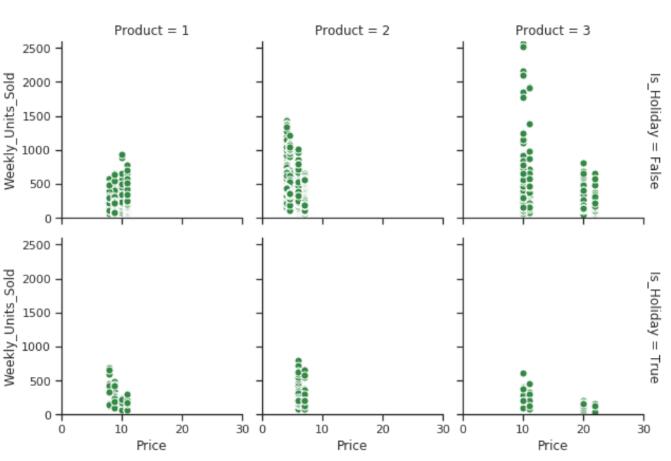
g = sns.FacetGrid(df, col="Product", row="Is_Holiday", margin_titles=True, height=3)
g.map(plt.scatter, "Price", "Weekly_Units_Sold", color="#338844", edgecolor="white", s=50, lw=1)
g.set(xlim=(0, 30), ylim=(0, 2600));
- 在假期和平日,每种产品都有多个价格。 我猜一个是正常价格,另一个是促销价格。
- 产品3的价格差距很大,在促销期间已削减至近50%。
- 在非节假日期间,产品3的销售额最高。
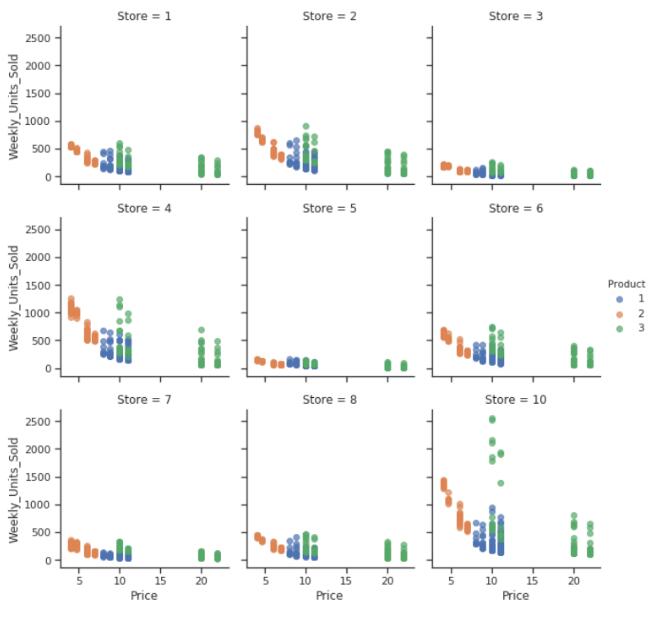
g = sns.FacetGrid(df, col="Store", hue="Product", margin_titles=True, col_wrap=3)
g.map(plt.scatter, 'Price', 'Weekly_Units_Sold', alpha=.7)
g.add_legend();
所有这9家商店都提供这3种产品。 它们似乎都具有类似的折扣促销。 但是,产品3在商店10促销期间的单位销售最多。
剩下的还有不少分析,我们这个暂时不看了,直接看结论吧:
- 最热闹和拥挤的商店是10号商店,最不拥挤的商店是5号商店。
- 就销售数量而言,最畅销的产品是全年的产品2。
- 商店不一定在假期期间进行产品促销。假期似乎对商店或产品销售没有影响。
- 产品2似乎是最便宜的产品,而产品3是最昂贵的产品。
- 大多数商店都有某种季节性,每年都有两个旺季。
- 2月份产品1的销售量比其他月份略多,4月份产品2的销售量最高,而7月份至9月份的产品3的销售量最高。
- 每个产品都有其正常价格和促销价格。产品1和产品2的正常价格和促销价格之间没有明显的差距,但是,产品3的促销价格可以削减到其原始价格的50%。尽管每个商店都对产品3进行了这种降价,但是商店10是降价期间销量最高的商店。
- 在促销期间卖出比平常更多的商品并不稀奇。商店10的产品3在7月至9月左右是最畅销的产品。
四、使用Prophet进行时间序列分析
我们将在商店10建立产品3的时间序列分析,并以美元为单位预测每周销售额。
store_10_pro_3 = df[(df.Store == 10) & (df.Product == 3)].loc[:, ['Base Price', 'Price', 'Weekly_Units_Sold', 'weekly_sales']]
store_10_pro_3.reset_index(level=0, inplace=True)
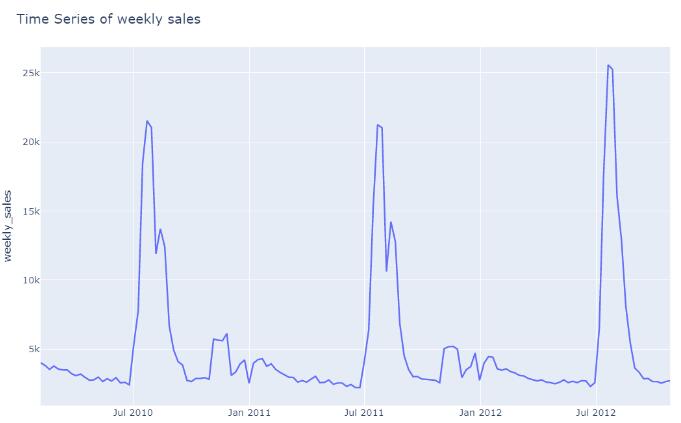
fig = px.line(store_10_pro_3, x='Date', y='weekly_sales')
fig.update_layout(title_text='Time Series of weekly sales')
fig.show()
商店10中产品2的季节性很明显。 在学校放假期间,销售总是在7月到9月之间达到顶峰。
下面我们执行Prophet模型,预测未来50周的每周销售量。
store_10_pro_3 = store_10_pro_3[['Date', 'weekly_sales']].rename(columns = {'Date': 'ds',
'weekly_sales': 'y'})
model = Prophet(interval_width = 0.95)
model.fit(store_10_pro_3)
future_dates = model.make_future_dataframe(periods = 50, freq='W')
forecast = model.predict(future_dates)
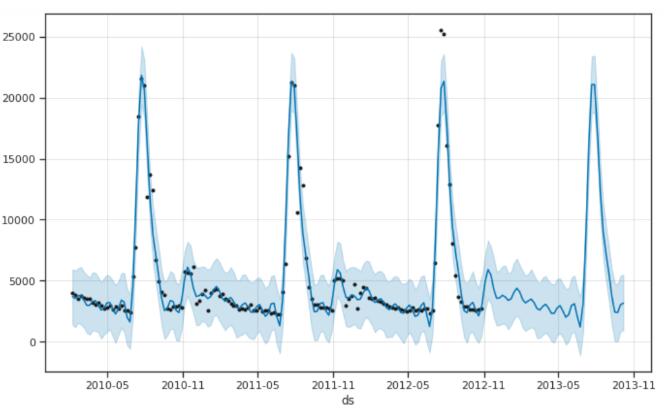
model.plot(forecast);
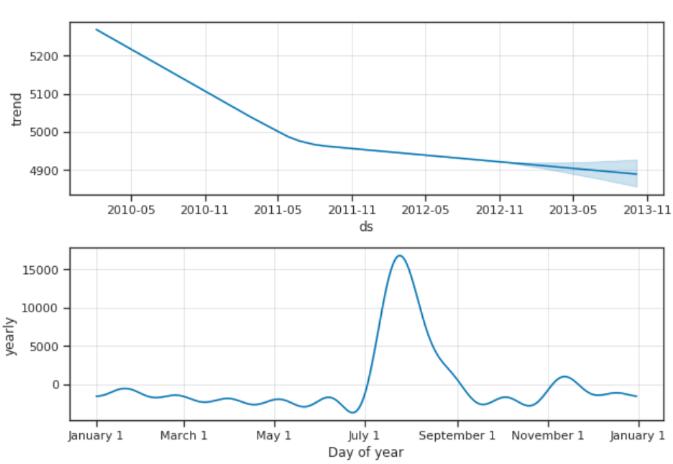
model.plot_components(forecast);
metric_df = forecast.set_index('ds')[['yhat']].join(store_10_pro_3.set_index('ds').y).reset_index()
metric_df.dropna(inplace=True)
error = mean_squared_error(metric_df.y, metric_df.yhat)
print('The RMSE is {}'. format(sqrt(error)))
最后得到的RMSE是1190.0962582193933
五、季节性的影响
Prophet一个很重要的能力是,们可以添加自己的自定义季节性。 在这里,我们将添加从7月初到9月初的学校假期。
def is_school_holiday_season(ds):
date = pd.to_datetime(ds)
starts = datetime.date(date.year, 7, 1)
ends = datetime.date(date.year, 9, 9)
return starts < date.to_pydatetime().date() < ends
store_10_pro_3['school_holiday_season'] = store_10_pro_3['ds'].apply(is_school_holiday_season)
store_10_pro_3['not_school_holiday_season'] = ~store_10_pro_3['ds'].apply(is_school_holiday_season)
model = Prophet(interval_width=0.95)
model.add_seasonality(name='school_holiday_season', period=365, fourier_order=3, condition_name='school_holiday_season')
model.add_seasonality(name='not_school_holiday_season', period=365, fourier_order=3, condition_name='not_school_holiday_season')
model.fit(store_10_pro_3)
forecast = model.make_future_dataframe(periods=50, freq='W')
forecast['school_holiday_season'] = forecast['ds'].apply(is_school_holiday_season)
forecast['not_school_holiday_season'] = ~forecast['ds'].apply(is_school_holiday_season)
forecast = model.predict(forecast)
plt.figure(figsize=(10, 5))
model.plot(forecast, xlabel = 'Date', ylabel = 'Weekly sales')
plt.title('Weekly sales forecast');
metric_df = forecast.set_index('ds')[['yhat']].join(store_10_pro_3.set_index('ds').y).reset_index()
metric_df.dropna(inplace=True)
error = mean_squared_error(metric_df.y, metric_df.yhat)
print('The RMSE is {}'. format(sqrt(error)))
结果发现RMSE是1127.4109974735834,略有下降。