有人把Metropolis算法当作是二十世纪最伟大的十大算法之一。这个算法是大规模抽样算法的一种，也叫做马尔可夫链蒙特卡洛（Markov chain Monte Carlo，MCMC）。对于很多高维问题来说，比如计算一个凸体的体积，MCMC仿真是目前唯一可以在合理时间内解决这个问题的一般性方法。
MCMC技术经常被用在解决高维空间中的积分和优化问题。这两类问题在机器学习、物理学、统计学、经济学和决策分析中扮演了一个很重要的角色。下面给出一些例子。
欢迎关注 DataLearner 官方微信，获得最新 AI 技术推送
给定一些未知变量$$x\in X$$，和数据$$y\in Y$$。下面是贝叶斯统计中非常典型的难以解决的积分问题。 a) 规范化：为了获取给定先验$$p(x)$$和似然函数$$p(y|x)$$条件下后验$$p(x|y)$$的结果，需要计算贝叶斯理论中的规范化因子：
p(x|y)=\frac{p(y|x)p(x)}{\int_{X}p(y|x')p(x')dx}
b) 边缘化：给定联合后验概率$$(x,z)\in X \times Z$$。我们感兴趣的是边缘后验概率：
p(x|y) = \int_{Z}p(x,z|y)dz
c) 期望：贝叶斯分析的一个主要目标就是获取统计量的形式：
E_{p(x|y)}(f(x))=\int_{X}f(x)p(x|y)dx
蒙特卡洛仿真的思想是从定义在高维空间中的目标密度函数$$p(x)$$中抽取独立同分布的样本$$\{x^{(i)}\}^{N}_{i=1}$$。这个N个样本可以使用下面的点质量函数来估计目标密度函数：
p_{N}(x)=\frac{1}{N}\sum_{i=1}^{N}\delta_{x^{(i)}}(x)
其中$$\delta_{x^{(i)}}$$表示狄拉克函数（delta-Dirac）。因而，我们可以使用非常容易处理的求和函数来计算$$I(f)$$的积分：
I_{N}(f)=\frac{1}{N}\sum_{i=1}^{N}f(x^{(i)}) \to \int_{X}f(x)p(x)dx
这里意味着对$$I_{N}(f)$$的估计是无偏的。而且，由于大数定理，它几乎可以确定收敛于$$I(f)$$。同时，如果$$f(x)$$的方差（为了简单起见，用一元为例）满足$$\sigma_{f}^{2}\cong E_{p(x)}(f^{2}(x))-I^{2}(f)<\infty$$，那么$$I_{N}(f)$$估计量的方差等于$$var(I_{N}(f)=\frac{\sigma_{f}^{2}}{N})$$。中心极限定理就可以产生如下的收敛：
\sqrt{N}(I_{N}(f)-I(f)) \Longrightarrow N(0,\sigma_{f}^{2})
因此，对于高维空间中的密度函数的计算可以通过抽取其独立同分布的样本进行。对于一些常见的分布，如高斯分布、Gamma分布我们都可以通过均匀分布抽取它们的样本，但对于一些复杂的形式我们无法通过传统方法抽样时，就可以通过MCMC方法进行计算了。
正如之前所说，对于给定的概率分布$$p(x)$$，我们通常都希望能有便捷的方式生成它对应的样本。也就是根据给定的分布进行抽样。对于简单的分布，如正态分布、多项式分布等等我们都可以通过一个均匀分布进行抽样。但当我们遇到一个比较复杂的概率分布的时候，简单抽样无法工作。这里就可以使用MCMC进行抽样了。
MCMC是在探索状态空间$$X$$时，使用马尔科夫链机制产生样本的方法。这种机制保证了链在最重要的区域内运行。实际上，这种机制保证了样本$$x^{(i)}$$会模仿从分布$$p(x)$$中抽取的样本。我们从马尔科夫链开始说明MCMC是如何工作的。 假设我们希望抽样的概率分布为P(X)，但是P(X)形式非常复杂，我们无法直接抽样。于是我们思考，如果我们能找出一个转移矩阵pi，使其目标分布（马氏链的平稳分布）为P(X)，那么我们给x任何一个初始值，使它沿着转移概率不停跳转，在马氏链收敛后我们就能得到平稳分布的样本，即P(x)的一个样本。 举个例子（来源），假设我们希望得到如下概率分布的样本：
假设我们的初始值是从0，1，2中各以1/3的概率进行选择。我们选择的转移概率如下
| Tables | xi+1 | xi | xi-1 | | ------------- |:-------------:| -----:| | xi<=9 | 1/2 | (10-xi)/20 |xi/20 | xi>9 | 5/(xi+1) | (xi-9)/(2(xi+1)) | 1/2
假设我们从0，1，2中以相等的概率抽取90个点（每个值有30个点）。那么第一次迭代后的结果可能是0有15个，1有30个，2有30个，3有15个。第二次迭代结果可能是0有7个，1有15+8=23个，2有15+15=30个，3有15+7=22个，4有8个……这样一直下去，最后90个点应当一上面的分布分布在各个点上。如下图所示：
请注意，这里的x0,x1,...并没有收敛，但是P（Xn=x）收敛了。但我们之观察链x0,x1，。。就行了。因此，只要给定一个转移矩阵，我们从任何一个初始状态出发，迭代足够多的次数后就可以得到目标分布的样本了。那么，如何寻找该转移矩阵呢？这就用到了马尔科夫链理论的知识了。
马尔科夫链 假设$$x^{(i)}$$是一个链中的第i个状态，当$$x^{(i)}$$只能取离散值的时候，我们很容易想到引入有限状态空间下的Markov链。随机过程$$x^{(i)}$$称为Markov链，当其满足：
p(x^{(i)}|x^{(i-1)},...,x^{(1)}) = p(x^{(i)}|x^{(i-1)})
这个式子的含义很简单，就是指马氏链任何一点的状态只与上一个状态有关，与之前的状态无关。这个式子在任何情况下都成立。在马尔科夫链中，只要给定一个转移矩阵，且该转移矩阵满足细致平衡条件（Detailed balance condition），那么从任意初始状态出发，经过足够多次迭代后，我们都可以得到一个稳定分布，该分布称为稳定分布（Stationary distribution）。我们举一个简单的例子。假设一个马氏链有三个状态(s=3)，转移矩阵假设是：
如果初始状态是$$\mu(x^{(1)})=(0.5,0.2,0.3)$$，那么经过T次迭代后，初始状态与转移矩阵相乘再与转移矩阵相乘至T次我们可以发现结果收敛于$$p(x)=(0.2,0.4,0.4)$$不再变化。
这个稳定后的结果在MCMC仿真中扮演了基础性角色。对于任意一个起始点，其结果都收敛于不变的分布$$p(x)$$。只要转移矩阵满足下面的条件：
用细致平衡条件得到平稳分布可以如下定义（细致平衡的物理含义就是从对于任何两个状态i,j，从i转移到j丢失的能量等于从j转移到i的获得的能量）：如果非周期马氏链的转移矩阵P和分布pi(x)满足如下条件
\pi(x^{(i)})P(x^{(i)}|x^{(j)})=\pi(x^{(j)})P(x^{(j)}|x^{(i)})
那么，$$\pi(x)$$就是该马氏链的平稳分布。证明也很简单，当我们把两边所有的$$x^{(i-1)}$$状态加和就可以得到：
\pi(x^{(i)})P=\sum_{x^{(i)}}\pi(x^{(j)})P(x^{(i)}|x^{(j)})=\pi(x^{(j)})\sum_{x^{(i)}}P(x^{(i)}|x^{(j)})=\pi(x^{(j)})
那么显然$$\pi(x^{(i)})$$已经是平稳分布了。但是一般情况下，我们很难确定一个好一个转移矩阵达到上述公式1的细致平衡条件，也就是上述公式左右并不相等。这时我们可以做一个改造，在公式两边引入一个概率$$\alpha(i,i-1)$$（这里我们以$$j=i-1$$为例）：
\pi(x^{(i)}) P(x^{(i)}|x^{(i-1)}) \alpha(i-1,i) = \pi(x^{(i-1)})P(x^{(i-1)}|x^{(i)}) \alpha(i,i-1)
最简单的取法就是等于$$\alpha(i-1,i)=\pi(x^{(i-1)})P(x^{(i-1)}|x^{(i)})$$，$$\alpha(i,i-1)=\pi(x^{(i)}) P(x^{(i)}|x^{(i-1)})$$。因此，转移矩阵就变成了$$\hat{P}=P(x^{(i)}|x^{(i-1)}) \alpha(i-1,i)$$。这里引入的$$\alpha(i-1,i)$$称为接收率。而$$Q=P(x^{(i)}|x^{(i-1)})$$成为建议分布（proposal distribution）（其实从这里可以看出来，建议分布的选择不影响收敛结果，因此，它可以选择任何分布，建议分布的选择只会影响收敛速度，根据MCMC with Metropolis-Hastings algorithm: Choosing proposal用户的回答，建议分布选择高斯分布的时候，这个算法就是我们通常所说的Metropolis算法，如果选择其他分布，那就是随机游走方法。对于Metropolis算法来说，如果方差较小，那么接受率就较高，算法的收敛速度就会变慢。事实上，如果方差较小，模型通常不会收敛）。
MCMC抽样是不可约的且没有周期性的马氏链，其目标分布是一个不变的分布。设计这种抽样器的一种方法是满足细致平衡条件。同时，让抽样器快速收敛也是非常重要的。实际上，我们大多数的努力都是为了加快收敛速度。 为了加快收敛速度，我们可以同步放大上述细致平衡条件左右两端，比如同时放大相同倍数。最大我们可以使其中一个转移概率达到1也就是可以取：
\alpha(i,i-1) = \min \{ \frac{p(x^{(i-1)})T(x^{(i)}|x^{(i-1)})}{p(x^{(i)}) T(x^{i-1}|x^{(i)})},1\}
光谱理论对这个问题有不错的帮助。注意到$$p(x)$$是矩阵T的特征向量，其特征值是1。实际上，线性代数中Perron-Frobenius定理告诉我们剩余的特征向量的特征值小于1。因此，第二大特征向量决定了收敛的速度，我们希望它越小越好。
不可约性、非周期性和不变性的概念如果对应到现实中，我们就很容易理解它们的角色了。当我们在互联网上搜索信息的时候，我们实际上是针对一组链接。我们可以把网页和链接比作是马氏链的转移图中的节点和有向边。显然，当我们在互联网上随机游走的时候我们希望避免陷入循环（非周期性），并且能够到达所有的页面（不可约性）。让我们现在考虑Google非常有名的PageRank算法。PageRank将转移矩阵定义成两个部分，$$T=L+E$$。L是大规模链接矩阵，其行和列都是网页。E则是小规模的均匀随机矩阵，目的是加到L后使其具有非周期性和不可约性。它是额外的噪音，避免我们陷入死循环，是我们总有一定概率跳转到其他页面。从之前的讨论，我们有：
p(x^{(i+1)})[L+E]=p(x^{i})
这里，不变的分布（特征向量）$$p(x)$$代表网页$$x$$的排名。注意到，我们也可以设计出更加有意思的转移矩阵。只要它满足不可约性和非周期性我们都可以将其引入转移矩阵中。 在连续状态空间中，转移矩阵T变成了一个积分核K，而且$$p(x)$$变成了相关的特征函数。
\int p(x^{(i)})K(x^{(i+1)}|x^{(i)})dx^{(i)} = p(x^{(i+1)})
这里的核心K是给定$$x^{(i)}$$值的条件下$$x^{(i+1)}$$的条件概率。这是马氏链算法的数学表达式。
Metropolis算法是在一个接受/拒绝规则下随机游走的一个变种，其收敛于一个指定的目标分布。算法的过程如下： 1、首先从起始分布$$p_0(\theta)$$中选择一个起始点$$\theta^0$$，且$$p(\theta^0 | y) > 0 $$。起始分布可以是一个近似分布，或者直接选择一个近似估计值。 2、对 t=1,2...，有： （a）在时间点t，从一个跳转分布jumping distribution（或者是建议分布proposal distribution）中抽取一个建议的$$\theta^{*}$$。在Metropolis算法（注意，不是Metropolis-Hastings算法）中，建议分布必须是对称的，即对于所有的$$\theta_a,\theta_b$$和时间$$t$$，满足条件$$J_t(\theta_a|\theta_b)=J_t(\theta_b|\theta_a)$$。 （b）计算密度比率
r = \frac { p(\theta^* | y) } { p(\theta^{t-1}|y)}
（c）以概率 $$\min\{r,1\}$$使$$\theta^t=\theta^*$$。否则$$\theta^t = \theta^{t-1}$$
给定当前值$$\theta^{t-1}$$时，马氏链的转移分布$$T_{t}(\theta^{t}|\theta^{t-1})$$是$$\theta^{t}=\theta^{t-1}$$出点质量的混合，跳转分布的一个带权重的版本会调整接收率。
这个算法需要可以计算上面步骤2中（b）的比率r，并且可以对所有的$$\theta$$和$$t$$都能抽取跳转分布的样本。跳转不成功也就是拒绝接受当前样本时，迭代次数依然会加1。
Metropolis-Hastings算法是最流行的MCMC方法。后面我们会看到，大部分实际的MCMC算法都是该方法的特例或者扩展。 不变分布$$p(x)$$和建议分布$$q(x^{*}|x)$$包括在给定当前值$$x$$的情况下，根据$$q(x^{*}|x)$$抽取候选样本。然后，马尔可夫链以概率$$A(x,x^{*})=\min\{1,[p(x)q(x^{*}|x)]^{-1}p(x^{*})q(x|x^{*})\}$$移动到$$x^{*}$$，否则仍然保持为$$x$$。伪代码如图5所示，图6显示了用MH算法解决建议分布（proposal distribution）为高斯分布$$q(x^{*}|x^{(i)})=N(x^{(i)},100)$$，目标为双峰分布$$p(x)\propto 0.3\exp(-0.2x^{2})+0.7\exp(-0.2(x-10)^2)$$的5000次迭代计算结果。如图所示，样本的频率直方图与目标分布近似。
MH算法非常简单，但是，对建议分布$$q(x^{*}|x)$$的设计需要非常小心。在接下来的部分中，我们将看到很多MCMC算法都是通过考虑设计选择特殊的建议分布达到要求的。一般情况下，我们可以使用次优的推断和学习算法来产生数据驱动的建议分布。 MH算法的转移核心为：
K_{MH}(x^{(i+1)}|x^{(i)})=q(x^{(i+1)}|x^{i})A(x^{(i)},x^{(i+1)})+\delta_{x^{(i)}}(x^{(i+1)})r(x^{(i)})
其中，$$r(x^{(i)})$$是与拒绝有关的项：
r(x^{(i)})=\int_{X}q(x^{*}|x^{(i)})(1-A(x^{(i)},x^{*}))dx^{*}
这里很容就能证明MH算法产生的样本是与从目标分布中抽取样本的方法很像。我们看到$$K_{MH}$$满足细致平衡条件：
p(x^{(i)})K_{MH}(x^{(i+1)}|x^{(i)})=p(x^{(i+1)})K_{MH}(x^{(i)}|x^{(i+1)})
因此，MH算法可以把$$p(x)$$当作不变分布。为了证明MH算法是收敛的，我们需要证明转移过程是非循环的且是不可约的（即可以通过有限步并以正向的概率转移）。首先，由于算法允许拒绝，所以它是非周期的。为了确保不可约性，我们需要确保$$q(\cdot)$$的支持度包含$$p(\cdot)$$的支持度。在这些条件下，我们就可以渐进收敛了。如果状态空间$$X$$是有限的，我们就可以使用极小值证明均匀遍历。同样，也可以使用Foster-Lyapunov漂移条件证明均匀遍历。（Under these conditions, we obtain asymptotic convergence (Tierney, 1994, Theorem 3, p. 1717). If the space X is small (for example, bounded in Rn), then it is possible to use minorisation conditions to prove uniform (geometric) ergodicity (Meyn & Tweedie, 1993). It is also possible to prove geometric ergodicity using Foster-Lyapunov drift conditions (Meyn & Tweedie, 1993; Roberts & Tweedie, 1996).）
独立采样器和Metroplolis Algorithm是MH算法两个简单的实例。独立采样器中，建议分布是独立于当前状态$$q(x^{*}|x^{(i)})=q(x^{*})$$的。因此，其接受的概率是
A(x^{(i)},x^{*}) = \min \{1,\frac{p(x^{*})q(x^{(i)})}{p(x^{(i)})q(x^{*})} \} = \min \{1,\frac{w(x^{*})}{w(x^{(i)})} \}
这个算法与重要性抽样很相似，但是，这里的样本是具有相关性的，因为它们来自于一个样本和另一个样本的比较。Metroplolis Algorithm则假设一个对称的随机游走建议分布$$q(x^{*}|x^{(i)})=q(x^{i}|x^{*})$$，因此，其接受的概率变成：
A(x^{(i)},x^{*}) = \min \{ 1, \frac{p(x^{*})}{p(x^{(i)})} \}
MH算法的有一些属性值得强调一下。首先，不需要目标分布的正规化常数。其次，尽管伪代码使用了单链，但很容易据此模仿出并行的独立链。最后，算法的成功与否依赖于建议分布的选择。这一点图7可以说明。不同的建议标准差$$\sigma^{*}$$的选择导致了不同的结果。如果建议的太小，那么$$p(x)$$可能只有一个模式。另一方面，如果太大，拒绝率会比较高，导致了很高的相关性。如果所有的模式的被遍历过，那么接受的概率会很高。我们说这样的链是混合的。
met1=function(iters)
{
xvec=numeric(iters)
x=1
for (i in 1:iters) {
xs=x+rnorm(1)
A=dgamma(xs,2,1)/dgamma(x,2,1)
if (runif(1)<A)
x=xs
xvec[i]=x
}
return(xvec)
}
iters=100000
out=met1(iters)
hist(out,freqmain
curvedgammaxaddcollwd
假设我们希望得到全局最大值，而不是近似的$$p(x)$$。比如说，如果$$p(x)$$是似然函数或者是后验分布，我们希望计算极大似然估计或者是极大后验估计。根据前面所说的，我们可以运行不变分布$$p(x)$$的马氏链从而通过如下式子估计全局最优：
\hat x = \arg\ \max_{x^{i};j=1,...,N}p(x^{(i)})
但这个方法缺乏效率，因为随机样本很少来自众数附近。除非分布在众数附近有较大的概率质量，计算资源会浪费在探索我们不感兴趣的区域。一个更加有原则的策略是采用模拟退火的方法。这项技术包含了模拟一个非参数马尔科夫链，它在第i次迭代处的不变分布不再是$$p(x)$$，但却有：
p_{i}(x) \propto p^{1/T_{i}}(x)
其中，$$T_{i}$$是冷却进度表，有$$\lim_{i\to \infty}T_{i}=0$$。这样做的原因是，$$p(x)$$在若规律性假设下，$$p^{\infty}(x)$$是一个集中在其全局最大值$$p(x)$$附近的概率密度。因此，如图8所示，模拟退火算法（simulated annealing）是标准MCMC算法的一个小小的改进。因此使用模拟退火算法解决之前的例子的结果如图9所示。 为了获取有效的退火算法，我们依然需要选择合适的建议分布和一个合适的冷却进度表。很多不好的退火算法都是由于不好的建议分布的设计。机器学习中逐渐兴起的复杂的变量和模型选择场景，我们甚至可以选择复杂的跳转MCMC核心（one can even propose from complex reversible jump MCMC kernels）。一旦我们定义好参数和模型空间，这项技术就可以用来搜寻最好的模型并同时进行极大似然参数估计。 大多数收敛的结果都会导致模拟退火算法，在给定$$T_{i}$$条件下，相似的马氏转移核会迅速混合，然后会在保证序列$$T_{i}=(C\ln(i+T_{0}))^{-1}$$的情况下，向$$p(x)$$的全局最大值集合收敛，这里的$$C$$和$$T_{0}$$依赖于问题而定。在有限空间或者简单的连续空间中，大多数结果都能被获得。
假设我们有一个n维向量x以及全条件表达式$$p(x_{j}|x_{1},...,x_{j-1},x_{j+1},...,x_{n})$$。在这种情况下，使用如下的建议分布非常有效：
q(x^{*}|x^{(i)}) = p(x^{*}_{j}|x^{(i)}_{-j})
当$$x_{-j}^{*}=x_{-j}^{(i)}$$时，其它时候左边等于0。相应的接受概率为：
A(x^{(i)},x^{*}) = \min\{1,\frac{p(x^{*})q(x^{(i)}|x^{*})}{p(x^{(i)})q(x^{*}|x^{(i)})} \} = = \min\{1,\frac{p(x^{*})p(x^{(i)}_{j}|x^{(i)}_{-j})}{p(x^{(i)})p(x^{*}_{j}|x^{*}_{-j})} \} = \min {1,\frac{p(x^{*}_{-j})}{p(x^{(i)}_{-j})}} = 1
因此，每一个建议的接受概率都是1，因此，Gibbs抽样的确定性的描述如表12。 由于Gibbs抽样可以看作MH算法的特例，将MH步骤引入Gibbs抽样中是可能的。也就是，当全条件存在且符合标准分布的形式（Gamma，Gaussian等），我们就可以直接抽取新样本。对于n=2的情况，Gibbs抽样也被称做数据扩张算法（data augmentation algorithm），它和EM算法很接近。 有向无环图（Directed acyclic graphs, DAGs）是Gibbs抽样最著名的应用领域。在这里，高维联合分布被分解成有向图。特别的，如果$$x_{pa(j)}$$节点是$$x_{i}$$节点的父节点，那么：
p(x) = \prod_{j}p(x_{j}|x_{pa(j)})
它满足如下形式的全条件的形式：
p(x_{j}|x_{-j})=p(x_{j}|x_{pa(j)})\prod_{k\in ch(j)} p(x_{k}|x_{pa(k)})
其中，$$ch(j)$$表示$$x_{j}$$的子节点。也就是说，我们只需要考虑父节点、子节点和子节点的父节点就好。这些变量被称为马尔科夫毯（Markov blanket）。这个技术是著名Gibbs抽样的贝叶斯更新软件（BUGS）的基础。使用Gibbs抽样器从全条件下抽样，使得它建立了一般目的的MCMC软件。
这段话可能比较难以理解，我们可以借助其他描述来理解。吉布斯抽样也称作是交替条件抽样。吉布斯抽样的每次迭代中我们都是一其他值为条件，抽取参数向量中一个参数。也就是说，假设我们的参数是$$\theta=(\theta_{1},...,\theta_{d})$$。那么每次迭代我们都有d个步骤。在每次迭代中，我们都会选定d个参数的序列，然后对于每个$$\theta_{j}^{t}$$都从基于其他$$\theta$$的条件概率进行样本抽取。
p(\theta_{j} | \theta^{t-1}_{-j},y)
其中$$\theta^{t-1}_{-j}$$表示除了$$\theta_{j}$$的所有参数。
举个例子，以二元正态分布为例。假设有一个二元正态总体，其均值$$\theta=(\theta_{1},\theta_{2})$$未知，协方差矩阵已知，$$(y_{1},y_{2})$$是来自该总体的一个观测值。假设均值的先验是均匀分布，后验分布为：
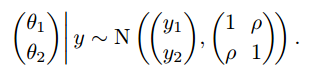
当然，这个例子中直接从联合后验分布$$\theta_{1},\theta_{2}$$也是很容易的。但为了说明吉布斯抽样，我们采取另外的方式。根据前面描述，我们每次迭代应该抽取每个$$\theta$$的条件概率：
\theta_1 | \theta_2,y \sim N(y_1 + \rho (\theta_2 - y_2 ), 1- \rho^2)
\theta_2 | \theta_1,y \sim N(y_2 + \rho (\theta_1 - y_1 ), 1- \rho^2)
每次迭代，吉布斯抽样只要根据上面两个式子分别抽取$$\theta_1$$和$$\theta_2$$的结果就可以了。
从迭代仿真中推断的基本方法和贝叶斯仿真是一样的：从$$p(\theta|y)$$中抽取的样本来概括后验密度，计算如分位数、各阶矩以及其他我们感兴趣的量。未观测量的后验预测仿真也可以通过仿真获得。这里我们讨论一些值得注意的东西。
#####4.1、从迭代仿真中进行推断的困难
迭代仿真有增加了仿真中两个问题。首先，迭代次数不足会导致样本无法代表目标分布，即便仿真达到了收敛近似条件，起初迭代的结果也只是反映了近似的分布而非目标分布。其次，迭代仿真中序列自己的相关性。除去收敛问题，从相关样本中进行仿真推断不如从独立样本进行推断精确。仿真序列中的相关性也不必须是一个问题，在收敛的地方，样本实际上就是呈现$$p(\theta|y)$$的分布。所以我们一般都忽略仿真样本的顺序。但这样的相关性会导致一些效率问题。 我们会从三个方面解决迭代仿真的问题：1）我们会设计仿真的程序以监控收敛情况，比如仿真多个序列。2）我们会监控不同关注量内在的方差和它们之间的方差知道它们大约相等。只有当每一个仿真序列和所有序列混合结果都相似的时候，它们才能代表目标分布。3）如果仿真的效率太慢，需要更换算法。
#####4.3、每个序列中迭代的依赖 #####4.4、拥有过分分散的起始点的多个序列 #####4.5、监控估计量的值 #####4.6、收敛监控的挑战 #####4.7、将每个保存的序列分成两部分 #####4.8、使用序列内和序列间的方差评估
来源1：An Introduction to MCMC for Machine Learning，CHRISTOPHE ANDRIEU，2003 来源2：Introduction to Markov chain Monte Carlo — with examples from Bayesian statistics 来源3：http://cos.name/2013/01/lda-math-mcmc-and-gibbs-sampling/