矩母函数简介(Moment-generating function)
64,364 阅读
在统计学中,矩母函数是一个关于随机变量的实值函数,它可以替代密度函数来描述分布。也就是说,出了概率密度函数外,我们也可以通过矩母函数来描述分布。对于某些概率密度函数和累计密度函数比较复杂的情况,我们使用矩母函数分析分布会大大降低复杂性,尤其是对于随机变量的加权求和来说,矩母函数可以提供非常简单的计算。当然,矩母函数出了是基于实值函数,也可以是基于向量和矩阵的,扩展性很好。但是,并不是所有的分布都存在矩母函数。
定义
在概率统计学中,某个随机变量$X$的矩母函数定义如下:
M_X(t) = E[e^{tX}], \space\space\space t\in R
当且仅当这个期望是存在的时候。换句话说,矩母函数可以认为是随机变量$e^{tX}$的期望。 $M_X(0)$永远存在,且必须等于1。定义这个函数的原因也是,通过这个函数,我们可以求出分布的所有高阶矩的结果,因为我们可以使用拉普拉斯变换。
e^{tX}=1+tX+\frac{t^2X^2}{2!} + \frac{t^3X^3}{3!} + \cdots +\frac{t^nX^n}{n!}
因此有:
\begin{aligned}
M_X(t) &= E[e^{tX}] = 1 + tE(X)+\frac{t^2E(X^2)}{2!} + \frac{t^3E(X^3)}{3!} + \cdots +\frac{t^nE(X^n)}{n!} \\
&\\
&= 1 + tm_1 + \frac{t^2m_2}{2!} + \frac{t^3m_3}{3!} + \cdots + \frac{t^nm_n}{n!}
\end{aligned}
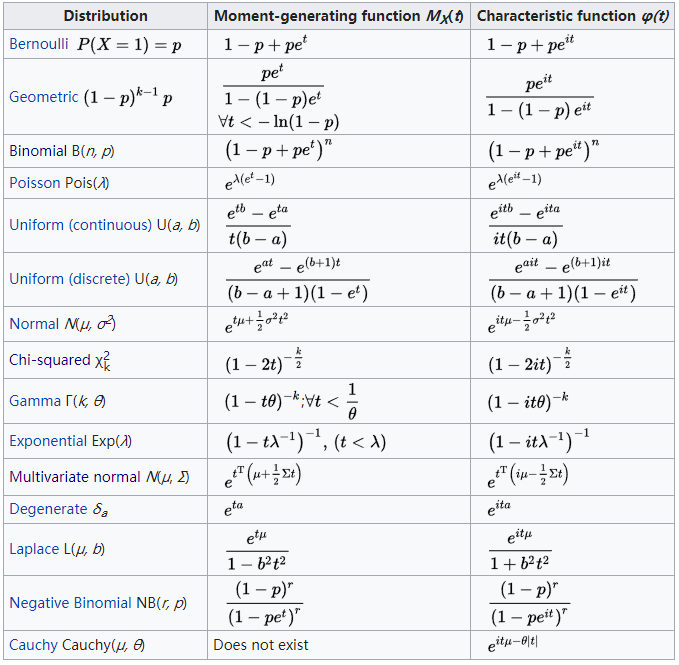
这里的$m_n$就是$n$-阶矩。 常见分布的矩母函数:
矩母函数的属性
1、矩母函数是正的且是log凸函数,其中M(0)=1 2、单值性,这是矩母函数最重要的一个性质。即当两个分布有相同的矩母函数的时候,这两个分布在所有点上的值都相同。即,如果:
M_X(t) = M_Y(t)
那么有:
F_X(x) = F_Y(y)
对于所有的$x$的值都成立。但是这句话不同于“如果两个分布具有相同的矩,那么他们在所有点上的值都相同”,因为某些情况下,矩存在,但是矩母函数不存在,因为有如下的限制:
\lim_{n\rightarrow \infty} \sum_{i=1}^n \frac{t^im_i}{i!}
这个式子的值可能是不存在的。log正态分布就是这个例子。
