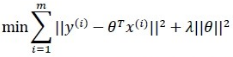机器学习之正则化项

刚刚开始接触推荐方面模型时，在建模中总能看到“正则化项”、“正则化系数”这样的名词，一开始以为这是建模中的惯用的手法，但是随着看着文献增加，慢慢发现正则化开始变得多样而神秘，模型中到底要不要加正则化呢？到底该选哪种正则化项呢？ （“正则化项(regularizer)”又叫做“惩罚项(penalty term)”）

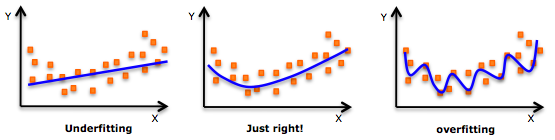
监督机器学习问题实际上就是在规则化参数的同时实现最小化误差，而最小化误差是为了让模型拟合训练数据，而规则化参数就是为了防止我们的模型过分拟合我们的训练数据。下面，我们来看一下拟合数据时的三种情况：

从左到右分别是欠拟合（underfitting，也称High-bias）、合适的拟合和过拟合（overfitting，也称High variance）三种情况。

以推荐问题中的贝叶斯评估问题为例，规则化项相当于贝叶斯模型的先验概率，可以是模型参数向量的范数。

上面的λ||θ||²便是正则化项，只不过这里用的是L2范数。正则化项可以是零范数、一范数、二范数、迹范数、Frobenius范数和核范数等。下面来具体看一下L0、L1、L2三种：

** L0范数是指向量中非0的元素的个数。 L1范数是指向量中各个元素绝对值之和。 L2范数是指向量各元素的平方和然后求平方根。**

**L0和L1都是参数是稀疏的。**L0范数来规则化一个参数矩阵的话，就是希望W的大部分元素都是0。但是，L0范数很难优化求解（NP难问题）。而L1范数是L0范数的最优凸近似，比L0范数要容易优化求解。所有，如果在研究建模时，如果隐特征中大多数与最终结果没多大关系的话，在训练模型时希望这些特征的权重尽可能为0的话，也就是想要使得整个矩阵变得稀疏的话，一般采取L1范数来正则化（不会采用L0范数使得每个特征权重都是非0的），这样就可以直观的判别出所有的特征中的重要特征。 L2范数在研究建模中是为了防止过拟合的，让L2范数的规则项||θ||²尽可能小，不断地进行权值衰减，也就是使参数矩阵的每个元素都很小，趋近于0，但不会像L1范数那样等于0。L1是让绝对值最小，L2是让平方最小，由此可知，L1的下降速度很快，L2范数在优化迭代时的下降是平缓稳定的，逐渐收敛到0附近。所以，在矩阵分解模型中，L0范数会产生较少的隐特征，很多特征的权值为0，而L2会产生更多一点，因为有一些特征是趋近0却不等于0的。

所以，综合这三种范数的特点来看的话：如果在建模时，特征数较多，而很多特征又与结果没有直接关系的话，想要参数矩阵变得稀疏的的话，就选择L1范数；如果在进行矩阵分解时，设定特征数量后，希望每个特征都能有一定的权重的话，那么就选择L2范数。 （在我遇到的BPR相关的推荐问题中，大部分选择L2范数来正则化。）