Dirichlet Tree Distribution(狄利克雷树分布)
这篇博客的主要内容来自于Tom Minka的笔记——The Dirichlet-tree distribution
####简介 Dirichlet分布作为多项式分布的先验已经很流行了,但是狄利克雷分布还有两个主要的限制: 1)每一个变量有自己的均值,但是它们却共享一个变量参数 2)除了限制它们的和为1外,变量之间必须相互独立。
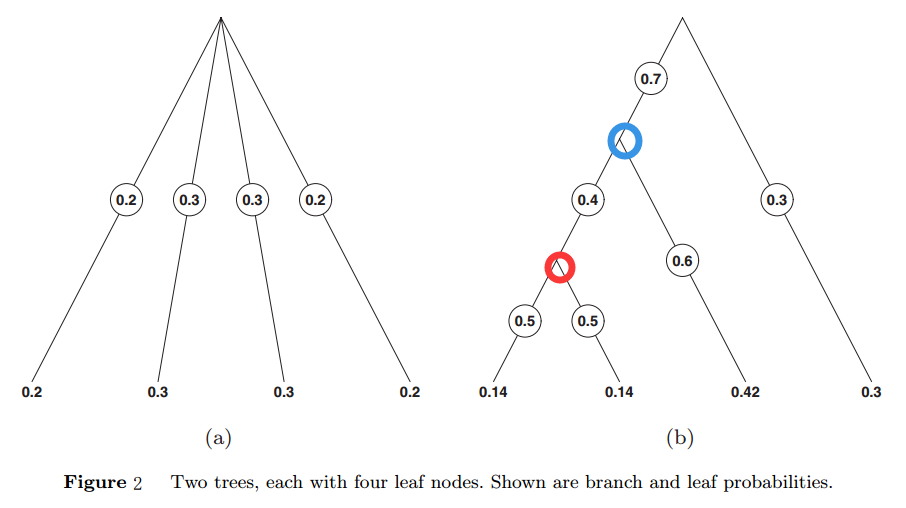
这里介绍的Dirichlet-tree分布可以克服上述缺点但保留计算上的简洁。新的分布也可以作为多项式分布的先验。在这里,我们不再把多项式分布的样本看作是一个K面的筛子结果,我们把它看作是一个有限的随机过程的结果。如图1中的(a)所示,一个叶子节点的概率是每个树枝所有的概率乘积。图1中的b图是更一般形式的树。在Dirichlet分布中,参数是叶子节点的概率,即$[p_1 \ldots p_K]$,所以某个样本x的概率为(注意:这里右上角$\delta(x-k)$是delta函数,又叫Dirac delta function。其值在任意范围内都是0,除了在0位置。因而这里的delta函数就表示当x取k的时候,$\delta(x-k)=1$,否则就是0,那么下式的含义就是某个点的概率就是对应的pk):