深度学习技巧之Padding

卷积神经网络是深度学习中处理图像的利器。在卷积神经网络中，Padding是一种非常常见的操作。本片博客将简要介绍Padding的原理。

首先，我们看一下正常的卷积操作：

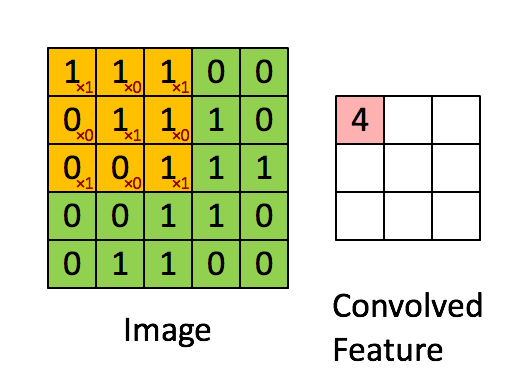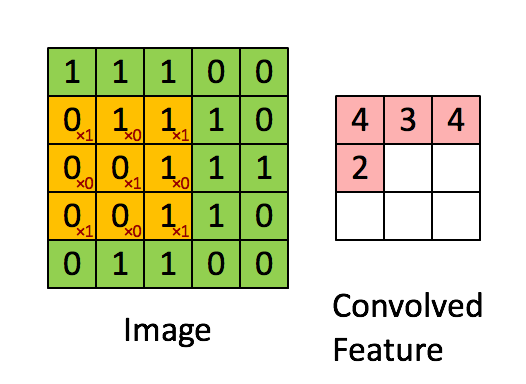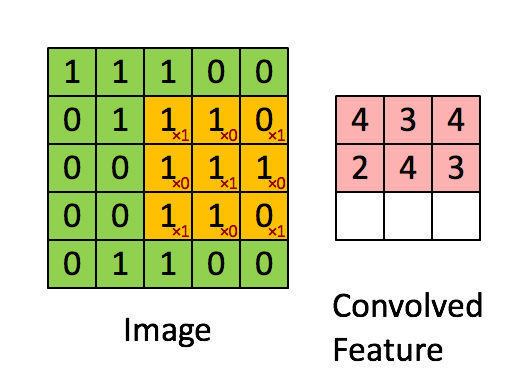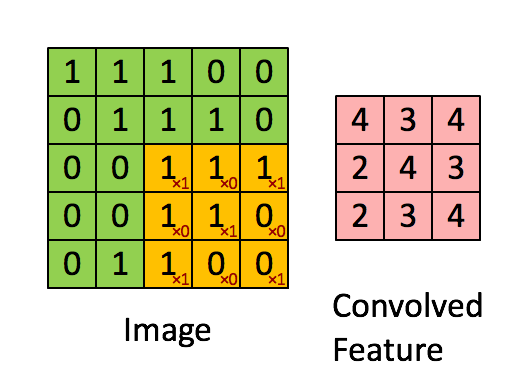
<center>![](https://cdn-images-1.medium.com/max/1600/1*ZCjPUFrB6eHPRi4eyP6aaA.gif)</center>
<center></center>

如上图所示，左图是一个5×5的图像（绿色），我们使用一个3×3的卷积核（kernal，或者是滤波器，filter）进行卷积操作（黄色），最终可以得到一个3×3的结果（右边的红色图像）。

使用卷积操作处理图像带来了两个问题：首先是图像由原来的5×5的矩阵变成了3×3的结果，这使得输入的图像缩小（shrink）了。在一个大型的卷积神经网络中，如果一个图像经过了几百次的卷积操作，那么会使得图片缩小的很厉害。其次，可以看到，这种扫描方式会使得边缘角落的像素被扫到的次数少于中间的像素。例如，左上角第一个像素1，自始至终只会被扫描到1次，而最中间的1会被扫描到9次。这种操作会使我们都是图片的边缘信息。

为了缓解上述问题，我们会对图片做填充操作（padding）。即在图片边缘加一条边。

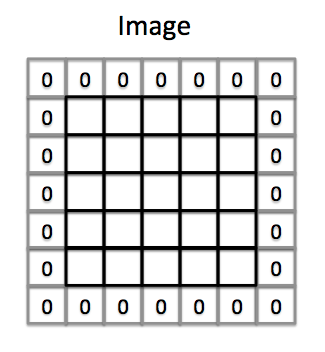
<center>![](https://cdn-images-1.medium.com/max/325/1*b77nZmPH15dE8g49BLW20A.png)</center>
<center></center>

这时候，原来的5×5的图像，就变成了7×7的图像了。继续使用上述3×3的卷积核扫描，最终会得到（7-3+1）=5×5的结果。假设原始图像是n×n，填充宽度为p，卷积核大小是f×f，那么卷积操作之后图像大小的结果是：

```math
(n+2 p-f+1) \times (n+2 p-f+1)
```

到这里也许有个疑问，就是padding的长度如何选择。这里一般有两个选择原则，一个是有效卷积（valid convolutions）和一个是不变卷积（same convolutions）。前一个其实就是不添加padding。后者就是添加一个padding长度使得卷积操作前后的图像大小一致。这时候padding长度结果是$p=\frac{f-1}{2}$。这里的f我们经常会看到都是奇数。实际上很难看到大家使用偶数的卷积核。这个原因可能有两个，一个是如果你选择偶数作为卷积核大小，会导致padding不对称。最后要么左边多一点要么右边多一点，很奇怪。另一个原因是如果使用奇数作为卷积核大小，那么卷积核正好有个最中心的点。这就很容易用来描述卷积核的位置。解释不算完美，但是是吴恩达coursera课程上给出的。

深度学习技巧之Padding

相关博客

最热博客