
时间序列数据处理中的相关数学概念
时间序列数据分析的基础包含大量的统计知识。这篇博客主要用通俗的语言描述时间序列数据中涉及到的一些基本统计知识。
聚焦人工智能、大模型与深度学习的精选内容,涵盖技术解析、行业洞察和实践经验,帮助你快速掌握值得关注的AI资讯。

时间序列数据分析的基础包含大量的统计知识。这篇博客主要用通俗的语言描述时间序列数据中涉及到的一些基本统计知识。


多项式分布是非常常见的分布,他是二项分布在多维上的推广。例如掷骰子结果中,1-6点出现的次数就是一个多项式分布。多项式分布在如主题建模中非常常见,本文将讲述多项式分布的贝叶斯推导过程。
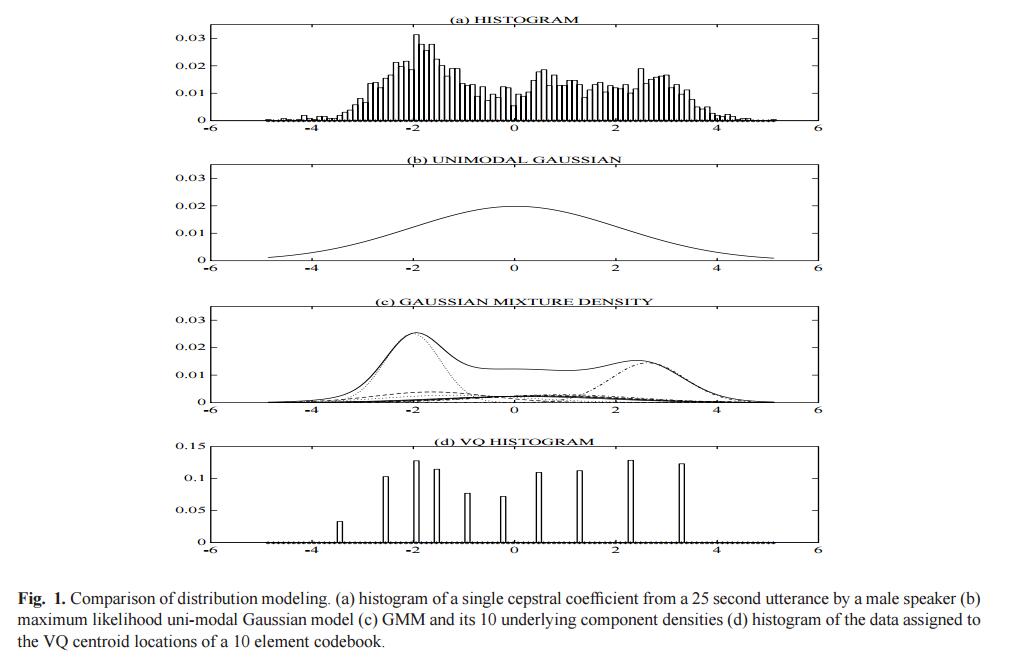
高斯混合模型是一个参数概率密度函数,它是一组高斯密度函数的加权求和。在生物统计领域,高斯混合模型通常是连续测度或者特征的概率分布的参数模型。高斯混合模型可以使用迭代的EM算法或者最大后验概率法估计参数。
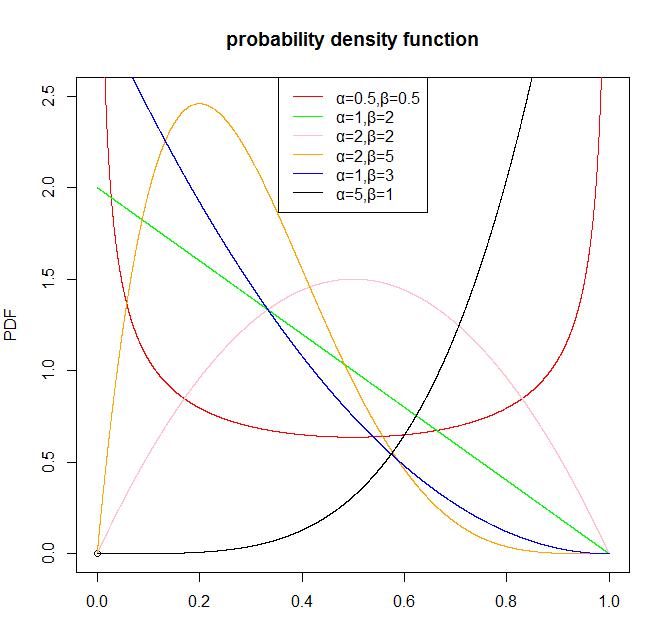
贝塔分布(Beta Distribution)是一个连续的概率分布,它只有两个参数。它最重要的应用是为某项实验的成功概率建模。在本篇博客中,我们使用Beta分布作为描述。
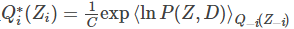
变分贝叶斯是一类用于贝叶斯估计和机器学习领域中近似计算复杂(intractable)积分的技术。它主要应用于复杂的统计模型中,这种模型一般包括三类变量:观测变量(observed variables, data),未知参数(parameters)和潜变量(latent variables)。

Wishart分布在多元高斯的贝叶斯推断中非常重要。它通常作为正态分布的协方差矩阵的逆矩阵的共轭先验存在。这篇博客将详细讲述Wishart分布及其作用。

多元正态(高斯)分布分布是我们最常用的分布之一,这篇博客的主要内容来自Will Penny的文章的翻译。主要讲述关于多元正态分布的贝叶斯推导
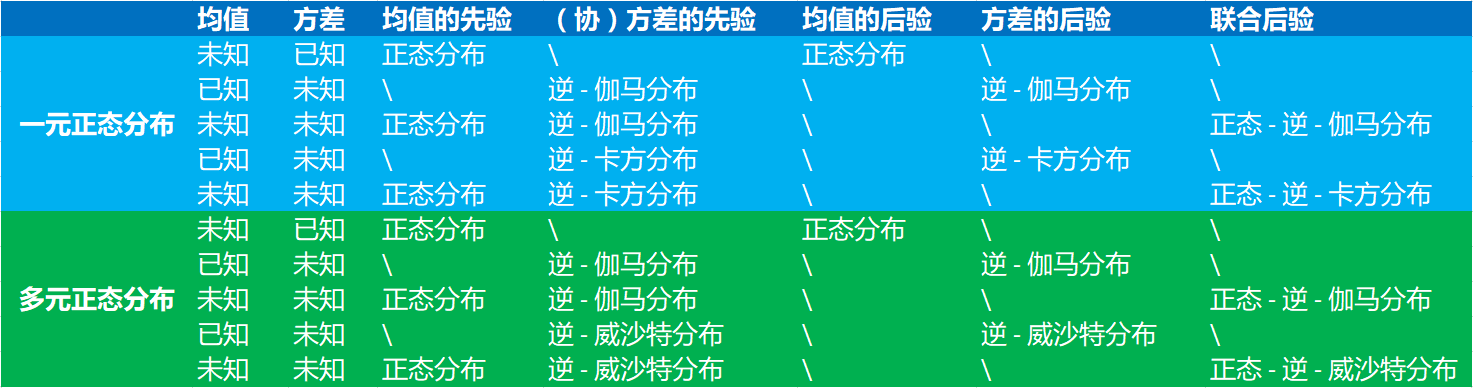
高斯分布是最常见的分布,也是数据挖掘和人工智能中相关统计学习方法所涉及到的最重要的分布之一。使用贝叶斯理论进行统计推断是目前最流行的推断方式。

抽取样本方差的分布可以帮助我们生成很多其他分布的样本,例如生成一元高斯分布的样本就是可以通过方差分布来产生。这篇博客将描述如何抽取样本方差的分布。
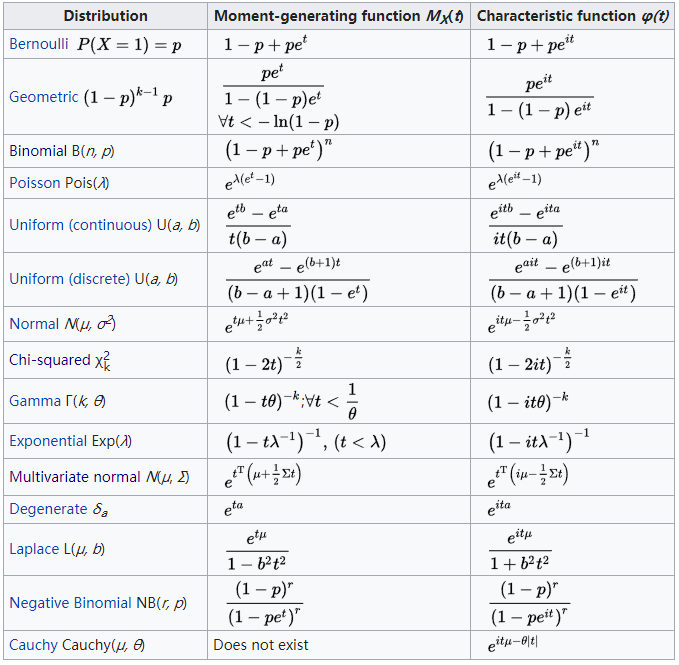
在统计学中,矩母函数是一个关于随机变量的实值函数,它可以替代密度函数来描述分布。也就是说,出了概率密度函数外,我们也可以通过矩母函数来描述分布。
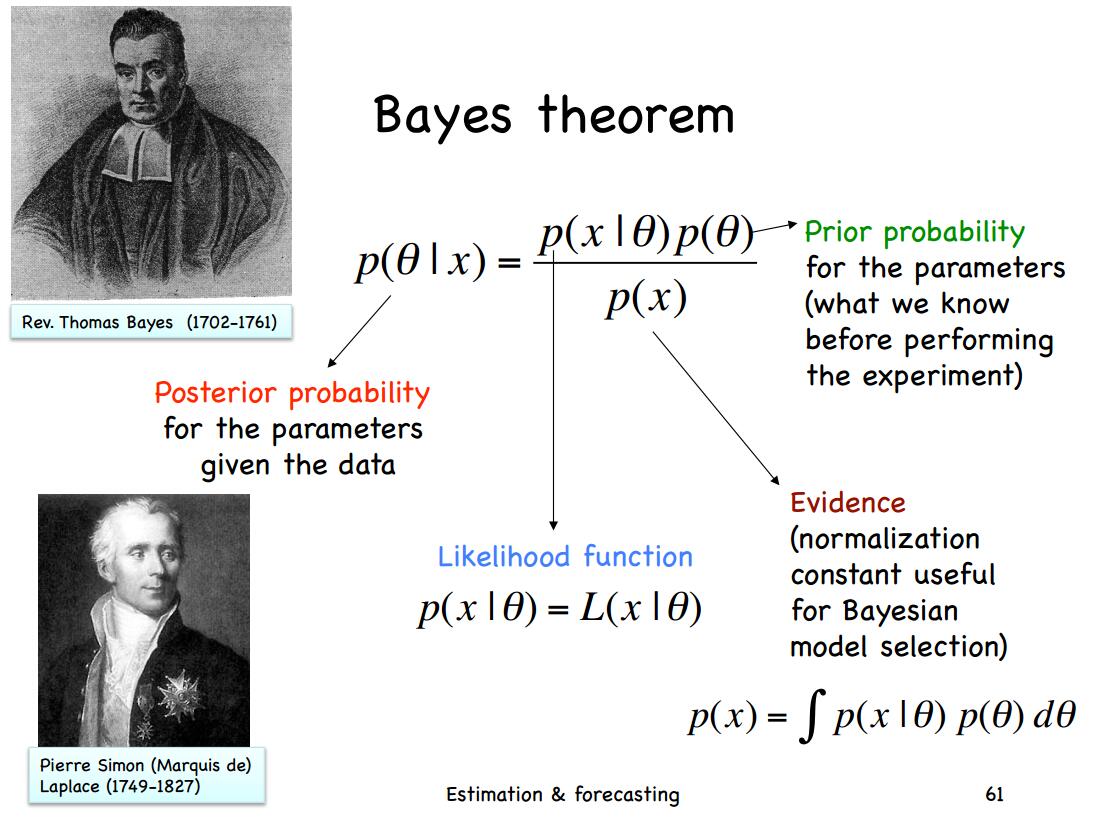
贝叶斯统计非常有用,也有一些基本的概念。这篇博客介绍了各种分布/概率的相关概念,并做了简单的介绍。

吉布斯抽样是贝叶斯推断中非常常用的方法。本文来自Cross Validated中一个人的回答。
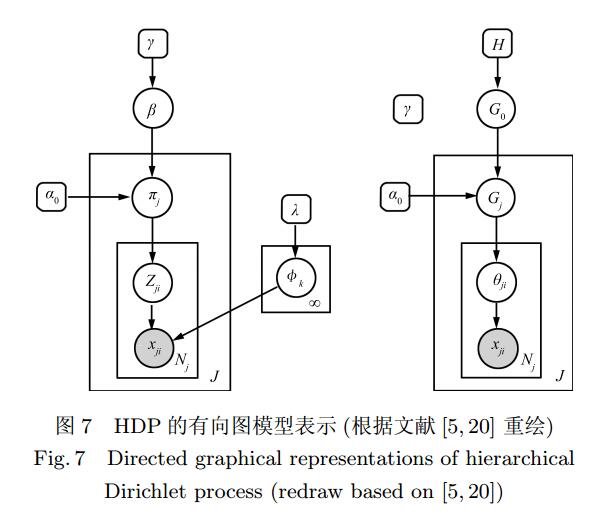
Dirichlet过程是一种重要的非参数模型,它可运用在聚类中,自动发现类别的数量。但很多时候,我们的工作都是具有层次话的。这篇文章介绍的层次狄利克雷模型就是解决这样的问题的。

狄利克雷分布作为多项式分布的先验大家应该比较熟悉了。这里介绍另外一种Dirichlet树结构的分布,也可以作为多项式分布的先验,但却更加灵活

EM(expectation-maximization)算法是统计学中求统计模型的最大似然和最大后验参数估计的一种迭代式算法,模型一般是依赖于不可观测的潜在变量。
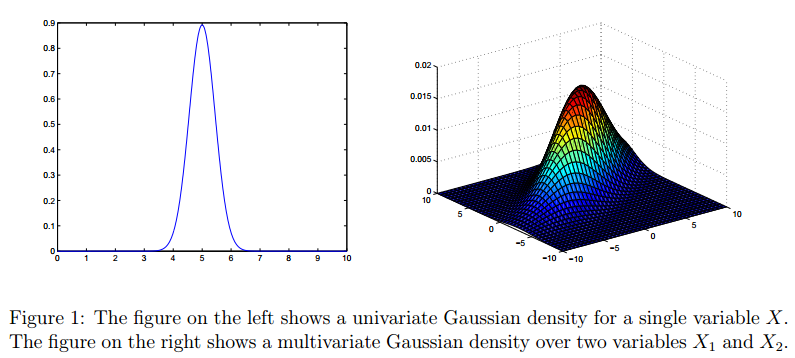
高斯分布是一种非常常见的分布,对于一元高斯分布我们比较熟悉,对于高斯分布的多元形式有很多人不太理解。这篇博客的材料主要来源Andrew Ng在斯坦福机器学习课的材料。

仿真抽样是给予贝叶斯方法第二春的重要角色。由于很多时候实际问题很复杂,我们无法精确求出后验密度,使用仿真抽样的方法我们可以获得近似的结果。这篇博客主要介绍了几种仿真抽样的方法。

这个系列的博客来自于 Bayesian Data Analysis, Third Edition. By. Andrew Gelman. etl. 的第五章的翻译。实际中,简单的非层次模型可能并不适合层次数据:在很少的参数情况下,它们并不能准确适配大规模数据集,然而,过多的参数则可能导致过拟合的问题。相反,层次模型有足够的参数来拟合数据,同时使用总体分布将参数的依赖结构化,从而避免过拟合问题。
关于高斯过程,其实网上已经有很多中文博客的介绍了。但是很多中文博客排版实在是太难看了,而且很多内容介绍也不太全面,搞得有点云里雾里的。因此,我想自己发表一个相关的内容,大多数内容来自于英文维基百科和几篇文章。

我们对层次贝叶斯推断的策略与一般的多参数问题一样,但由于在实际中层次模型的参数很多,所以比较困难。在实际中,我们很难画出联合后验概率分布的图形。但是,我们可以使用近似的基于仿真的方法。 在这个部分,我们提出一个联合了分析的和数值的方法从联合后验分布p(θ, φ|y)中获取仿真结果,以 小鼠肿瘤实验的beta-binormial模型为例,总体分布是p(θ|φ),与似然函数p(y|θ)是共轭的。对于很多非共轭层次模型,更高级的算法将在后面叙述。即使针对更复杂的问题,使用共轭分布来获取近似估计也是很有用的。

这个系列的博客来自于 Bayesian Data Analysis, Third Edition. By. Andrew Gelman. etl. 的第五章的翻译。实际中,简单的非层次模型可能并不适合层次数据:在很少的参数情况下,它们并不能准确适配大规 模数据集,然而,过多的参数则可能导致过拟合的问题。相反,层次模型有足够的参数来拟合数据,同 时使用总体分布将参数的依赖结构化,从而避免过拟合问题。本节将讲述互换性并建立层次模型